This commit is contained in:
@@ -1,5 +1,5 @@
|
|||||||
<div align="center">
|
<div align="center">
|
||||||
<h2>NEXT.JS LEXICAL BLOG</h2>
|
<h2>妙妙网站</h2>
|
||||||
</div>
|
</div>
|
||||||
|
|
||||||
<div align="center">
|
<div align="center">
|
||||||
|
|||||||
@@ -1,5 +1,5 @@
|
|||||||
<div align="center">
|
<div align="center">
|
||||||
<h2>NEXT.JS LEXICAL BLOG</h2>
|
<h2>lixiyu.net</h2>
|
||||||
</div>
|
</div>
|
||||||
|
|
||||||
<div align="center">
|
<div align="center">
|
||||||
|
|||||||
@@ -18,9 +18,9 @@ export const FriendLinkList = (props: { friends: TFriendItem[] }) => {
|
|||||||
<Separator />
|
<Separator />
|
||||||
<div className="my-2 flex flex-col justify-start text-base">
|
<div className="my-2 flex flex-col justify-start text-base">
|
||||||
<div className="mx-auto">
|
<div className="mx-auto">
|
||||||
{"Welcome to exchange our friend links and every high-quality blog websites are welcomed. "}
|
{"欢迎你和我交换友情链接。"}
|
||||||
<Link className="underline" href={`mailto:${Config.SocialLinks.email}`}>
|
<Link className="underline" href={`mailto:${Config.SocialLinks.email}`}>
|
||||||
{"Email me please"}
|
{"请邮件联系我"}
|
||||||
</Link>
|
</Link>
|
||||||
</div>
|
</div>
|
||||||
</div>
|
</div>
|
||||||
|
|||||||
@@ -9,7 +9,7 @@ export const HomeCover = () => {
|
|||||||
className="mt-5 mb-20 flex w-full justify-center rounded-xl"
|
className="mt-5 mb-20 flex w-full justify-center rounded-xl"
|
||||||
style={{
|
style={{
|
||||||
aspectRatio: "4/1",
|
aspectRatio: "4/1",
|
||||||
background: `url(${Config.PageCovers.websiteCoverURL})`,
|
background: `url(${Config.PageCovers.websiteCoverURL})` + " no-repeat center center",
|
||||||
backgroundSize: "cover",
|
backgroundSize: "cover",
|
||||||
}}
|
}}
|
||||||
>
|
>
|
||||||
|
|||||||
@@ -27,9 +27,6 @@ export const Footer = () => {
|
|||||||
>
|
>
|
||||||
{"Source Code"}
|
{"Source Code"}
|
||||||
</Link>
|
</Link>
|
||||||
<Link href="/sponsor" title="Sponsor me for my works.">
|
|
||||||
{"Sponsor"}
|
|
||||||
</Link>
|
|
||||||
<Link href="/friends" title="My friend links.">
|
<Link href="/friends" title="My friend links.">
|
||||||
{"Friends"}
|
{"Friends"}
|
||||||
</Link>
|
</Link>
|
||||||
|
|||||||
@@ -8,17 +8,17 @@ import { MdMenu, MdOutlineDarkMode, MdOutlineLightMode, MdSearch } from "react-i
|
|||||||
|
|
||||||
const MenuItems = [
|
const MenuItems = [
|
||||||
{
|
{
|
||||||
title: "HOME",
|
title: "主页",
|
||||||
href: "/",
|
href: "/",
|
||||||
},
|
},
|
||||||
{
|
{
|
||||||
title: "POSTS",
|
title: "日记",
|
||||||
href: "/posts",
|
href: "/posts",
|
||||||
},
|
},
|
||||||
{
|
// {
|
||||||
title: "ABOUT",
|
// title: "关于",
|
||||||
href: "/about",
|
// href: "/about",
|
||||||
},
|
// },
|
||||||
];
|
];
|
||||||
|
|
||||||
export const NavBar = () => {
|
export const NavBar = () => {
|
||||||
|
|||||||
@@ -14,4 +14,4 @@ export const PostURL = (postId: string) => `https://${Config.SiteDomain}/blog/${
|
|||||||
export const SearchURL = (keyword: string) => `https://${Config.SiteDomain}/search/?q=${keyword}`;
|
export const SearchURL = (keyword: string) => `https://${Config.SiteDomain}/search/?q=${keyword}`;
|
||||||
|
|
||||||
const year = getCurrentTime().year;
|
const year = getCurrentTime().year;
|
||||||
export const CopyrightAnnouncement = `COPYRIGHT © ${Config.YearStart === year ? year : `${Config.YearStart}-${year}`} ${Config.AuthorName} ALL RIGHTS RESERVED`;
|
export const CopyrightAnnouncement = `版权 © ${Config.YearStart === year ? year : `${Config.YearStart}-${year}`} ${Config.AuthorName} 版权所有`;
|
||||||
|
|||||||
@@ -4,14 +4,14 @@ export const Config: TConfig = {
|
|||||||
// Image url for avatar.
|
// Image url for avatar.
|
||||||
AvatarURL: "/images/avatar.webp",
|
AvatarURL: "/images/avatar.webp",
|
||||||
// Your favorite motto, or a brief self-introduction, for homepage display
|
// Your favorite motto, or a brief self-introduction, for homepage display
|
||||||
Sentence: "L'homme est né libre, et partout il est dans les fers.",
|
Sentence: "绿叶兮素华,芳菲菲兮袭予。",
|
||||||
// Your nickname, or pen name here.
|
// Your nickname, or pen name here.
|
||||||
Nickname: "John Doe",
|
Nickname: "妙妙",
|
||||||
|
|
||||||
// Website main title.
|
// Website main title.
|
||||||
SiteTitle: "LEXICAL BLOG",
|
SiteTitle: "妙妙日记",
|
||||||
// Your domain for website.
|
// Your domain for website.
|
||||||
SiteDomain: "nextjs-lexical-blog-demo.vercel.app",
|
SiteDomain: "lixiyu.net",
|
||||||
|
|
||||||
// For the cover image displayed on the homepage, the recommended image aspect ratio is 4:1.
|
// For the cover image displayed on the homepage, the recommended image aspect ratio is 4:1.
|
||||||
PageCovers: {
|
PageCovers: {
|
||||||
@@ -20,19 +20,7 @@ export const Config: TConfig = {
|
|||||||
|
|
||||||
// Your social platform IDs, and email address.
|
// Your social platform IDs, and email address.
|
||||||
SocialLinks: {
|
SocialLinks: {
|
||||||
twitter: "example", // Twitter ID
|
email: "lixiyua@gmail.com", // Email address, required.
|
||||||
instagram: "example", // Instagram ID
|
|
||||||
linkedin: "example", // Linkedin ID
|
|
||||||
github: "example", // Github ID
|
|
||||||
facebook: "example", // Facebook ID
|
|
||||||
youtube: "example", // Channel ID
|
|
||||||
reddit: "example", // Reddit ID
|
|
||||||
bilibili: "123456", // Bilibili Number ID
|
|
||||||
weibo: "123456", // Weibo UID
|
|
||||||
telegram: "example", // Telegram ID
|
|
||||||
quora: "example", //Quora ID
|
|
||||||
mastodon: "https://mas.to/@example", // Mastodon link
|
|
||||||
email: "me@example.com", // Email address, required.
|
|
||||||
},
|
},
|
||||||
|
|
||||||
// Giscus Configure. Please refer to the https://giscus.app for entire instruction
|
// Giscus Configure. Please refer to the https://giscus.app for entire instruction
|
||||||
@@ -82,7 +70,7 @@ export const Config: TConfig = {
|
|||||||
},
|
},
|
||||||
|
|
||||||
// Website establishment year.
|
// Website establishment year.
|
||||||
YearStart: "2023",
|
YearStart: "2025",
|
||||||
// Please enter your legal name for use with the copyright mark.
|
// Please enter your legal name for use with the copyright mark.
|
||||||
AuthorName: "JOHN DOE",
|
AuthorName: "jimlee & miaomiao(lixiyu)",
|
||||||
};
|
};
|
||||||
|
|||||||
@@ -2,12 +2,8 @@ import type { TFriendItem } from "@/types/friend.type";
|
|||||||
|
|
||||||
export const FriendsList: TFriendItem[] = [
|
export const FriendsList: TFriendItem[] = [
|
||||||
{
|
{
|
||||||
title: "但为君故's Blog",
|
title: "dev.2ha.me",
|
||||||
url: "https://dreams.plus/",
|
url: "https://dev.2ha.me",
|
||||||
},
|
|
||||||
{
|
|
||||||
title: "Your Best Friend's Blog",
|
|
||||||
url: "https://www.example.com/",
|
|
||||||
},
|
},
|
||||||
{
|
{
|
||||||
title: "Google",
|
title: "Google",
|
||||||
|
|||||||
@@ -1,118 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Some basic bash-script code block"
|
|
||||||
time: "2022-11-29"
|
|
||||||
tags: ["linux"]
|
|
||||||
summary: "Some basic bash-script code example. It might be help if writing some temporary work-scripts."
|
|
||||||
---
|
|
||||||
|
|
||||||
### Assignment and Substitution
|
|
||||||
|
|
||||||
```bash
|
|
||||||
a=375
|
|
||||||
hello=$a
|
|
||||||
```
|
|
||||||
|
|
||||||
### Variables
|
|
||||||
|
|
||||||
1. Built-in Variables
|
|
||||||
For example `$HOME $PWD ...`, for more info, see [environ(7)](https://man7.org/linux/man-pages/man7/environ.7.html)
|
|
||||||
2. Positional Parameters
|
|
||||||
**echo** $para1 $para2 $para3 $para4 $0 $1 $2 $3 $4 $@
|
|
||||||
3. Special Parameters
|
|
||||||
$? # exit status of a command, function, or the script itself
|
|
||||||
|
|
||||||
### Branches
|
|
||||||
|
|
||||||
```bash
|
|
||||||
if [ condition1 ];then
|
|
||||||
command_series1
|
|
||||||
elif [ condition2 ];then
|
|
||||||
command_series2
|
|
||||||
else
|
|
||||||
default_command_series3
|
|
||||||
fi
|
|
||||||
```
|
|
||||||
|
|
||||||
### Loops
|
|
||||||
|
|
||||||
### range for
|
|
||||||
|
|
||||||
```bash
|
|
||||||
for arg in `seq 10`; do
|
|
||||||
echo $arg
|
|
||||||
done
|
|
||||||
```
|
|
||||||
|
|
||||||
### for in C-like syntax
|
|
||||||
|
|
||||||
```bash
|
|
||||||
LIMIT=10
|
|
||||||
for ((a=1; a<=LIMIT; a++)); do
|
|
||||||
echo "$a "
|
|
||||||
done
|
|
||||||
```
|
|
||||||
|
|
||||||
### **while**
|
|
||||||
|
|
||||||
```bash
|
|
||||||
LIMIT=10
|
|
||||||
a=1
|
|
||||||
while ((a<=LIMIT)); do
|
|
||||||
echo "$a "
|
|
||||||
((a += 1))
|
|
||||||
done
|
|
||||||
```
|
|
||||||
|
|
||||||
### IO
|
|
||||||
|
|
||||||
```bash
|
|
||||||
command < input-file > output-file # rewrite
|
|
||||||
command >> output-file # appending
|
|
||||||
```
|
|
||||||
|
|
||||||
### Function
|
|
||||||
|
|
||||||
```bash
|
|
||||||
# define a function
|
|
||||||
function fun_name(){
|
|
||||||
command...
|
|
||||||
}
|
|
||||||
## or
|
|
||||||
fun_name(){ # arg1 arg2 arg3
|
|
||||||
command...
|
|
||||||
}
|
|
||||||
|
|
||||||
|
|
||||||
# apply a function
|
|
||||||
fun_name $arg1 $arg2 $arg3
|
|
||||||
|
|
||||||
|
|
||||||
# dereference
|
|
||||||
fun_name(){ # arg1
|
|
||||||
eval "$1=hello"
|
|
||||||
}
|
|
||||||
fun_name arg1
|
|
||||||
## the above code block is equivalent to
|
|
||||||
arg1=hello
|
|
||||||
```
|
|
||||||
|
|
||||||
### Debugging
|
|
||||||
|
|
||||||
1. take good use of sh(1)
|
|
||||||
for example:
|
|
||||||
sh -n script: checks for syntax
|
|
||||||
sh -v script: echo each command before executing it
|
|
||||||
sh -x script: echo the result of each command in an abbreviated manner
|
|
||||||
2. use echo
|
|
||||||
3. use trap
|
|
||||||
|
|
||||||
### Parallel
|
|
||||||
|
|
||||||
use GNU parallel
|
|
||||||
|
|
||||||
### Script with Style
|
|
||||||
|
|
||||||
1. Comment your code
|
|
||||||
2. Avoid using magic number
|
|
||||||
3. Use exit codes in a systematic and meaningful way
|
|
||||||
4. Use standardized parameter flags for script invocation
|
|
||||||
@@ -1,38 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Operating System Notes: Two Methods of Multiprocessor Scheduling"
|
|
||||||
time: "2022-12-05"
|
|
||||||
tags: ["OS"]
|
|
||||||
summary: "An introduction to two methods of multiprocessor scheduling is given: symmetric multiprocessing and asymmetric multiprocessing."
|
|
||||||
---
|
|
||||||
|
|
||||||
Two methods of multiprocessor scheduling
|
|
||||||
|
|
||||||
The first is **asymmetric multiprocessing (AMP).** The method is to have one processor handle the code for system activities (IO, scheduling decisions, etc.) in a processor cluster, and this processor becomes the main processor. Other processors execute user program code. This method is relatively simple, and because the main processor is only dedicated to processing system code, it can alleviate the need for data sharing.
|
|
||||||
|
|
||||||
The second type is **Symmetric multiprocessing (SMP).** It requires each processor to have self-scheduling function. And for the situation of ready queue and process execution, this method has two different implementation methods under subdivision.
|
|
||||||
|
|
||||||
First, each processor has a private ready queue for a process.
|
|
||||||
|
|
||||||
The second is to establish a common ready queue for all processes.
|
|
||||||
|
|
||||||
The above two approaches must ensure a premise, that is, you must be very careful when scheduling, implement a precise scheduling algorithm, check the ready queue, pop up a process and execute it before executing the process for each processor. If multiple processors want to access a common data area, it must be ensured that the process will not disappear from the queue. There will also be no situation where two processors execute the same process. Otherwise, processes may be missing or executed repeatedly, resulting in unpredictable errors.
|
|
||||||
|
|
||||||
Now operating systems, such as Linux, Windows, Mac OS, etc., all use the SMP method.
|
|
||||||
|
|
||||||
## Processor affinity
|
|
||||||
|
|
||||||
For operating systems that use the SMP method, processor affinity must be added to ensure the efficiency of the processor processing process. Because when a process is executed in the processor, a cache is usually established in the processor to use the data in the processor multiple times to reduce duplication of work and improve efficiency. But when the process migrates between different processors, To disable the cache in the original processor, rebuild the cache in the new processor. However, the cost and expense of doing so will increase dramatically, causing work efficiency to decrease. Therefore, the operating system should try its best to ensure that the process is only executed in one processor and avoid multiple migrations to different processors. This measure is called processor affinity. Simply put, make a process affinity to a processor.
|
|
||||||
|
|
||||||
However, there are two mandatory executions of affinity. One is **soft affinity**. The operating system tries its best to make the process be processed in one processor, but it cannot guarantee whether it will be migrated. The other is **hard affinity**, which forces a process to be processed only in one processor and does not allow migration between different processors. For example, the Linux system implements a hard affinity policy.
|
|
||||||
|
|
||||||
## Load balancing
|
|
||||||
|
|
||||||
For systems that use the SMP method, in a processor cluster, if the processors are unevenly idle, some processes can be extracted from the busy processors to idle processors to achieve overall work idleness. Busy balancing improves processor resource utilization. This is the load balancing strategy.
|
|
||||||
|
|
||||||
In the above, according to the allocation of ready queues, there are two methods of establishing a public ready queue and establishing a private ready queue for each processor. **Load balancing is usually not necessary if there is a public ready queue.** Because a process can be pulled from the public queue and allocated to an idle processor at any time. However, in most modern operating systems, private ready queues are established for different processors. It is necessary to use load balancing, regularly check the load of each processor, and migrate processes on overloaded processors to unloaded processors. middle. The migration of a process from an overloaded processor to an idle processor is called **push migration**. Pulling an idle processor from an overloaded processor into a process is called pull migration.
|
|
||||||
|
|
||||||
In fact, load balancing will eliminate the advantages brought by processor affinity due to process migration. Therefore, processor affinity and load balancing have certain opposing effects. This requires designing a better scheduling algorithm.
|
|
||||||
|
|
||||||
## Symmetric multithreading
|
|
||||||
|
|
||||||
Symmetric multi-threading technology is also known as **Hyper-Threading Technology (SMT)**. This is implemented in the hardware technology of the processor and does not belong to the operating system technology. The main idea is to logically divide a real physical processor into several logical processors, so that a physical processor is divided into functionally logically multiple processors, and each logical processor is responsible for its own process work. If the operating system can use divided logical processors to run processes, it can design specific scheduling algorithms to fully utilize processor resources and achieve greater performance.
|
|
||||||
@@ -1,68 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Resource Lock in Concurrency"
|
|
||||||
time: "2023-04-15"
|
|
||||||
tags: ["OS"]
|
|
||||||
summary: "Analysis and usage scenarios of spin lock, optimistic lock, pessimistic lock, read-write lock, mutex lock and other concepts."
|
|
||||||
---
|
|
||||||
|
|
||||||
## Spin lock
|
|
||||||
|
|
||||||
### Concept
|
|
||||||
|
|
||||||
**Spin Lock** is a lock mechanism based on busy waiting. Its implementation idea is to check in a loop whether the status of the lock is available when acquiring the lock. If the lock is occupied, it will wait in a loop. , until the lock is released. A spin lock is a non-blocking lock because it does not block the thread like a mutex lock, but waits in a loop until the lock is acquired.
|
|
||||||
Spin locks are mainly used to protect critical sections because they can achieve efficient thread synchronization on multi-core CPUs. Especially when competition in critical sections is not fierce, spin locks can reduce the cost of thread context switching, thereby improving the performance of the program. performance.
|
|
||||||
The implementation of a spin lock is very simple. An integer variable is usually used to represent the status of the lock. When the lock is occupied, the value of the variable is 1, and when the lock is available, the value of the variable is 0. During the process of acquiring the lock, the thread will continuously check the lock status in a loop until it finds that the lock is available, then sets the lock status to 1 and returns success. When the lock is released, the thread resets the lock's status to 0, allowing other threads to acquire the lock.
|
|
||||||
It should be noted that although spin locks can reduce the cost of thread context switching, when competition in the critical section is fierce, the efficiency of spin locks will become worse because it will cause threads to be busy waiting, wasting CPU resources.
|
|
||||||
|
|
||||||
The spin lock will keep busy waiting when the resource is occupied, and continuously loop to check whether the resource is available until the resource is obtained. On multi-core CPUs, spin locks can be implemented using atomic operation instructions such as CAS (Compare And Swap) provided by the hardware, thereby avoiding lock competition and the overhead of thread context switching. On a single-core CPU, the efficiency of the spin lock may be relatively low because it will always occupy CPU resources, causing other threads to be unable to execute. Therefore, in practical applications, it is necessary to select an appropriate lock mechanism according to the specific situation.
|
|
||||||
|
|
||||||
Therefore, in practical applications, it is necessary to select an appropriate lock mechanism according to the specific situation.
|
|
||||||
|
|
||||||
### Usage
|
|
||||||
|
|
||||||
Spin lock is a lock mechanism based on busy waiting. It continuously checks whether the shared resource is occupied while waiting for the shared resource to be released. If the shared resource is already occupied, wait until the shared resource is released; if the shared resource is not occupied, lock and access the shared resource. Spin lock is suitable for the following scenarios:
|
|
||||||
|
|
||||||
1. Occupation of shared resources in a short period of time: When shared resources are occupied for a short period of time and the waiting time is short, using spin locks can avoid the overhead of threads entering sleep state and thread context switching, thereby improving program performance. .
|
|
||||||
2. The number of threads accessing shared resources is small: Spin locks are suitable for situations where the number of threads accessing shared resources is small, because when the number of threads accessing shared resources is large, the busy waiting of spin locks will consume a lot of CPU resources. , resulting in reduced program performance.
|
|
||||||
3. Hardware support: Spin locks require hardware support to implement busy waiting, so they are suitable for systems using multi-processors or multi-core processors. It should be noted that spin locks are not suitable for scenarios with long waiting times, because long busy waiting will consume a large amount of CPU resources, resulting in system performance degradation. In the case of long waiting time, other lock mechanisms should be used, such as mutual exclusion locks, read-write locks, etc.
|
|
||||||
|
|
||||||
## Read-write lock
|
|
||||||
|
|
||||||
### Concept
|
|
||||||
|
|
||||||
**Read-Write Lock**, also known as shared-exclusive lock, is a special lock mechanism that allows multiple threads to read shared resources at the same time, but only allows one thread to write to shared resources . Read-write locks can effectively improve the concurrency performance of the program, especially when read operations are more frequent than write operations, it can reduce lock competition and improve the concurrency performance of the program.
|
|
||||||
The implementation of read-write lock is very simple, usually using a counter and a mutex lock to represent the lock status. When a thread wants to read a shared resource, it will first try to acquire a read lock. If no thread currently holds a write lock, the read operation can continue. If a thread holds a write lock, the read operation must wait for the write lock to be released. When a thread wants to write to a shared resource, it will first try to obtain a write lock. If no thread currently holds a read lock or write lock, the write operation can continue. If a thread holds a read or write lock, the write operation must wait for all read and write locks to be released.
|
|
||||||
It should be noted that although read-write locks can improve the concurrency performance of the program, the advantages of read-write locks may be weakened when write operations are frequent. Because each write operation must wait for both the read lock and the write lock to be released, the read operation will also be blocked, affecting the performance of the program. Therefore, in practical applications, it is necessary to select an appropriate lock mechanism according to the specific situation.
|
|
||||||
|
|
||||||
### Usage
|
|
||||||
|
|
||||||
Read-write lock is a special lock mechanism that allows multiple threads to read shared resources at the same time, but when writing to shared resources, they must be mutually exclusive. Read-write locks are suitable for the following scenarios:
|
|
||||||
|
|
||||||
1. There are far more read operations than write operations: When there are far more read operations than write operations, read-write locks can be used to improve the concurrency performance of the program. Read-write locks allow multiple threads to read shared resources at the same time, thereby reducing mutual exclusion competition between threads and improving the concurrency performance of the program.
|
|
||||||
2. The reading operation of shared resources is time-consuming: When the reading operation of shared resources is time-consuming, read-write locks can be used to improve the performance of the program. Read-write locks allow multiple threads to read shared resources at the same time, thereby reducing mutual exclusion competition between threads and the cost of thread context switching, and improving program performance.
|
|
||||||
3. There are fewer write operations on shared resources: When there are fewer write operations on shared resources, read-write locks can be used to improve the concurrency performance of the program. Read-write locks must be mutually exclusive when writing to shared resources, but multiple threads are allowed to do so at the same time when reading shared resources, thereby reducing mutual exclusion competition between threads and improving the concurrency performance of the program. It should be noted that read-write locks are suitable for scenarios where there is more reading and less writing. When the ratio of read-write operations is close, the performance of read-write locks may not be as good as that of mutex locks. In addition, when using read-write locks, you need to pay attention to the lock granularity to avoid the lock granularity being too fine or too coarse, which will affect the performance of the program.
|
|
||||||
|
|
||||||
## Mutex lock
|
|
||||||
|
|
||||||
### Concept
|
|
||||||
|
|
||||||
**Mutex (Mutex)** is the most basic lock mechanism, which can ensure that only one thread can access shared resources at the same time. When using a mutex lock, when one thread acquires the lock, other threads must wait for this thread to release the lock before they can acquire the lock. This can avoid data competition and inconsistency problems caused by multiple threads modifying shared resources at the same time.
|
|
||||||
Mutex locks are usually implemented using two operations: lock and unlock. When a thread wants to access a shared resource, it needs to first try to acquire the lock. If no other thread currently holds the lock, the thread can obtain the lock and access the shared resource. If another thread holds the lock, that thread must wait for the lock to be released. After the access is complete, the thread needs to release the lock so that other threads can obtain the lock and access the shared resource.
|
|
||||||
It should be noted that although using a mutex lock can ensure that only one thread can access shared resources at the same time, frequent locking and unlocking will cause program performance to decrease, because locking and unlocking operations require the overhead of system calls and kernel switching. . Therefore, in practical applications, mutex locks need to be used with caution to avoid excessive lock competition and lock waiting.
|
|
||||||
|
|
||||||
### Usage
|
|
||||||
|
|
||||||
Mutex lock is a common lock mechanism that ensures that only one thread can access shared resources at the same time, thereby avoiding mutual exclusion competition between threads. Mutex locks are suitable for the following scenarios:
|
|
||||||
|
|
||||||
1. Occupation of shared resources in a short period of time: When shared resources are occupied for a short period of time and the waiting time is short, using a mutex lock can avoid the overhead of threads entering sleep state and thread context switching, thereby improving program performance. .
|
|
||||||
2. The number of threads accessing shared resources is small: Mutex locks are suitable for situations where the number of threads accessing shared resources is small, because when the number of threads accessing shared resources is large, competition for mutex locks will become fierce, resulting in The performance of the program decreases.
|
|
||||||
3. There is less code in the critical section: Mutex lock is suitable for situations where there is less code in the critical section, because when there is more code in the critical section, the competition for the mutex lock will become fierce, resulting in a decrease in program performance.
|
|
||||||
4. Strong demand for synchronization: Mutex lock is suitable for situations where synchronization demand is strong, because it can ensure that only one thread can access shared resources at the same time, thereby avoiding mutual exclusion competition and data conflicts between threads. It should be noted that when mutex locks are used in a multi-threaded environment, deadlocks and other problems may occur. Therefore, issues such as lock granularity and locking order need to be considered to avoid deadlocks and other problems. In addition, when using mutex locks, you need to pay attention to lock performance issues to avoid excessive use of mutex locks, which may lead to program performance degradation.
|
|
||||||
|
|
||||||
## Optimistic locking and pessimistic locking
|
|
||||||
|
|
||||||
Optimistic locking and pessimistic locking are two different locking mechanisms used to solve data competition problems when accessing shared resources concurrently.
|
|
||||||
**Pessimistic locking is a pessimistic idea. It believes that in a concurrent environment, shared resources can easily be modified by other threads. Therefore, a lock must be locked every time a shared resource is accessed to ensure that only one thread can access the shared resource at the same time. .** The representative of pessimistic lock is a mutex lock, which can ensure that only one thread can access shared resources at the same time. However, locking and unlocking are expensive, **and can easily lead to a decrease in program performance.**
|
|
||||||
|
|
||||||
Optimistic locking is an optimistic idea. **It believes that in a concurrent environment, shared resources are rarely modified by other threads. Therefore, each time a shared resource is accessed, it is not locked. Instead, the shared resource is read first** and Check the version number and other information of the shared resource before modifying it. If it has not been modified, modify it and update the version number and other information. Otherwise, give up the modification and try again. Optimistic locks are represented by operations such as lock-free programming and CAS (Compare And Swap), which can reduce lock competition and thread context switching overhead, and improve the concurrency performance of the program.
|
|
||||||
It should be noted that although optimistic locking can improve the concurrency performance of the program, when shared resources are modified frequently concurrently, the number of retries of the optimistic lock may increase, resulting in a decrease in program performance. Therefore, in practical applications, it is necessary to select an appropriate lock mechanism according to the specific situation.
|
|
||||||
@@ -1,630 +0,0 @@
|
|||||||
---
|
|
||||||
title: "C/C++ Cross-Platform Compile-Macros"
|
|
||||||
tags: ["C", "C++"]
|
|
||||||
time: "2023-11-05"
|
|
||||||
summary: "When we compile some cross -platform programs, we will inevitably encounter _win32 __linux__ what is the macro of the compiler or the compiler environment.It indicates some information of the current platform environment to the compiler."
|
|
||||||
---
|
|
||||||
|
|
||||||
When we compile some cross -platform programs, we will inevitably encounter \_win32 , **Linux** What are the macroscopic macro of the compiler environment.There are many differences between \_win32 and win32 before.But there is a list here, making a memo.
|
|
||||||
|
|
||||||
For example, a code that can only be compiled under the Unix-Like platform in a set.If you compile the wrong error on the non-Unix-Like platform, then my code can add a macro to check whether it is a UNIX environment.If it is normally compiled, the error is thrown directly.
|
|
||||||
|
|
||||||
```text
|
|
||||||
#ifndef __unix__
|
|
||||||
#error This program should be complied and work in UNIX-LIKE platform.
|
|
||||||
#endif
|
|
||||||
```
|
|
||||||
|
|
||||||
The complete code is as follows:
|
|
||||||
|
|
||||||
```c
|
|
||||||
#ifndef __unix__
|
|
||||||
#error This program should be complied and work in UNIX-LIKE platform.
|
|
||||||
#endif
|
|
||||||
|
|
||||||
#include <stdio.h>
|
|
||||||
|
|
||||||
int main()
|
|
||||||
{
|
|
||||||
printf("this is unix-like platform");
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
This code can be compiled normally in the Mac OS and Linux environments, and an error will be reported under Windows.
|
|
||||||
|
|
||||||
---
|
|
||||||
|
|
||||||
**Below is a macro list of a detection environment.**
|
|
||||||
|
|
||||||
Please send updates/corrections to <u><a href="mailto:predef-contribute@lists.sourceforge.net">predef-contribute</a></u>.
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/AIX_operating_system">AIX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ----------- | ----------------------- |
|
|
||||||
| Identification | \_AIX | |
|
|
||||||
| Version | \_AIX'VR' | V = VersionR = Revision |
|
|
||||||
| Identification | **TOS_AIX** | Defined by xlC |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
If `_AIX` is defined, then the following macros can be used to determine the version. Notice that the macros indicates the mentioned version or higher. For example, if `_AIX43` is defined, then `_AIX41` will also be defined.
|
|
||||||
|
|
||||||
| AIX Version | Macro |
|
|
||||||
| ----------- | ------------ |
|
|
||||||
| 3.2.x | \_AIX3_AIX32 |
|
|
||||||
| 4.1 | \_AIX41 |
|
|
||||||
| 4.3 | \_AIX43 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Android_%28operating_system%29">Android</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | --------------- | ------ | ------------------------------------------------------------ |
|
|
||||||
| Identification | **ANDROID** | | |
|
|
||||||
| Version | **ANDROID_API** | V | V = API VersionMust be included from \<android/api-level.h\> |
|
|
||||||
|
|
||||||
Notice that Android is based on Linux, and that the Linux macros also are defined for Android.
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| Android Version | **ANDROID_API** |
|
|
||||||
| --------------- | --------------- |
|
|
||||||
| 1.0 | 1 |
|
|
||||||
| 1.1 | 2 |
|
|
||||||
| 1.5 | 3 |
|
|
||||||
| 1.6 | 4 |
|
|
||||||
| 2.0 | 5 |
|
|
||||||
| 2.0.1 | 6 |
|
|
||||||
| 2.1 | 7 |
|
|
||||||
| 2.2 | 8 |
|
|
||||||
| 2.3 | 9 |
|
|
||||||
| 2.3.3 | 10 |
|
|
||||||
| 3.0 | 11 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/UTS_%28Mainframe_UNIX%29">Amdahl UTS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----- |
|
|
||||||
| Identification | UTS |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/AmigaOS">AmigaOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ----------- | ---------------- |
|
|
||||||
| Identification | AMIGA | |
|
|
||||||
| Identification | **amigaos** | Defined by GNU C |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Domain/OS">Apollo AEGIS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----- |
|
|
||||||
| Identification | aegis |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Domain/OS">Apollo Domain/OS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------ |
|
|
||||||
| Identification | apollo |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Bada_%28operating_system%29">Bada</a></u>**
|
|
||||||
Based on Nucleus OS.
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/BeOS">BeOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------- |
|
|
||||||
| Identification | **BEOS** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Bluegene">Blue Gene</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ---------------- | -------------------------------------------------- |
|
|
||||||
| Identification | **bg** | All Blue Gene systemsDefined by XL C/C++ and GNU C |
|
|
||||||
| Version | **bgq** | Blue Gene/QDefined for XL C/C++ and GNU C |
|
|
||||||
| Identification | **THW_BLUEGENE** | All Blue Gene systemsDefined by XL C/C++ |
|
|
||||||
| Version | **TOS_BGQ** | Blue Gene/QDefined by XL C/C++ |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Bsd">BSD Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | ------------------------------------------------------------- | ------ | ---------------------------------------------------------- |
|
|
||||||
| Identification | **FreeBSD\_\_**NetBSD\_**\_OpenBSD\_\_**bsdi\_**\_DragonFly** | | |
|
|
||||||
| Version | BSD | YYYYMM | YYYY = YearMM = MonthMust be included from \<sys/param.h\> |
|
|
||||||
| Version | BSD4_2BSD4_3BSD4_4 | | Must be included from \<sys/param.h\> |
|
|
||||||
| Identification | \_SYSTYPE_BSD | | Defined by DEC C |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| Version | BSD | Macro |
|
|
||||||
| ------------ | ------ | ------ |
|
|
||||||
| 4.3 Net2 | 199103 | |
|
|
||||||
| 4.4 | 199306 | BSD4_4 |
|
|
||||||
| 4.4BSD-Lite2 | 199506 | |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/BSD/OS">BSD/OS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------- |
|
|
||||||
| Identification | **bsdi** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Convex_Computer">ConvexOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ---------- |
|
|
||||||
| Identification | **convex** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Cygwin">Cygwin Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ---------- |
|
|
||||||
| Identification | **CYGWIN** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Data_General">DG/UX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------- |
|
|
||||||
| Identification | DGUX |
|
|
||||||
| Identification | **DGUX** |
|
|
||||||
| Identification | **dgux** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/DragonFly_BSD">DragonFly</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------------- |
|
|
||||||
| Identification | **DragonFly** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Dynix">DYNIX/ptx</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | --------- |
|
|
||||||
| Identification | _SEQUENT_ |
|
|
||||||
| Identification | sequent |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/ECos">eCos</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------- |
|
|
||||||
| Identification | \_\_ECOS |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/EMX_%28programming_environment%29">EMX Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------- |
|
|
||||||
| Identification | **EMX** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Freebsd">FreeBSD</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | ------------------- | ------ | --------------------------------- |
|
|
||||||
| Identification | **FreeBSD** | | |
|
|
||||||
| Identification | **FreeBSD_kernel** | | From FreeBSD 8.3, 9.1, and 10.0.1 |
|
|
||||||
| Version | BSD | | |
|
|
||||||
| Version | **FreeBSD** | V | V = Version |
|
|
||||||
| Version | \_\_FreeBSD_version | ? | Must be included from osreldate.h |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| FreeBSD | **FreeBSD** | \_\_FreeBSD_version |
|
|
||||||
| ----------- | ----------- | ------------------- |
|
|
||||||
| 1.x | 1 | |
|
|
||||||
| 2.0-RELEASE | 2 | 119411 |
|
|
||||||
| 2.2-RELEASE | 2 | 220000 |
|
|
||||||
| 3.0-RELEASE | 3 | 300005 |
|
|
||||||
| 4.0-RELEASE | 4 | 400017 |
|
|
||||||
| 4.5-RELEASE | 4 | 450000 |
|
|
||||||
|
|
||||||
For more information see the <u><a rel="nofollow noreferrer" class="wrap external" href="http://www.freebsd.org/doc/en_US.ISO8859-1/books/porters-handbook/freebsd-versions.html">FreeBSD porters handbook</a></u>.
|
|
||||||
**GNU aka <u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/GNU/Hurd">GNU/Hurd</a></u>**
|
|
||||||
The official name of this operating system is GNU. Hurd is the kernel in the GNU operating system. It is often listed as GNU/Hurd since there is also GNU/Linux and GNU/kFreeBSD, which are most of the GNU operating system with the Linux and FreeBSD kernels respectively.
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------------- |
|
|
||||||
| Identification | **GNU** 1 |
|
|
||||||
| Identification | **gnu_hurd** 1 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/GNU/kFreeBSD">GNU/kFreeBSD</a></u>**
|
|
||||||
GNU/kFreeBSD is one of the Debian distros that is based on the FreeBSD kernel rather than the Linux or Hurd kernels.
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------------------------------- |
|
|
||||||
| Identification | **FreeBSD_kernel** && **GLIBC** |
|
|
||||||
|
|
||||||
Notice that FreeBSD also defines `__FreeBSD_kernel__` so the `__GLIBC__` macro must be checked to distinguish it.
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/GNU/Linux">GNU/Linux</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------------- |
|
|
||||||
| Identification | **gnu_linux** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/HI-UX">HI-UX MPP</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----------- |
|
|
||||||
| Identification | \_\_hiuxmpp |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/HP-UX">HP-UX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | -------- | ----------------- |
|
|
||||||
| Identification | \_hpux | Defined by HP UPC |
|
|
||||||
| Identification | hpux | |
|
|
||||||
| Identification | \_\_hpux | |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/IBM_i">IBM OS/400</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | --------- |
|
|
||||||
| Identification | **OS400** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Integrity_%28operating_system%29">INTEGRITY</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------------- |
|
|
||||||
| Identification | \_\_INTEGRITY |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Interix">Interix Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ----------- | ---------------------------------- |
|
|
||||||
| Identification | \_\_INTERIX | Defined by GNU C and Visual Studio |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Irix">IRIX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------- |
|
|
||||||
| Identification | sgi |
|
|
||||||
| Identification | \_\_sgi |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Linux_kernel">Linux kernel</a></u>**
|
|
||||||
Systems based on the Linux kernel define these macros. There are two major Linux-based operating systems: <u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/GNU/Linux">GNU/Linux</a></u> and<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Android">Android</a></u>, and numerous others like <u><a rel="nofollow noreferrer" class="wrap external" href="http://www.angstrom-distribution.org/">Ångström</a></u> or <u><a rel="nofollow noreferrer" class="wrap external" href="http://www.openembedded.org/">OpenEmbedded</a></u>
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | --------- | ------------------------------ |
|
|
||||||
| Identification | **linux** | 1 |
|
|
||||||
| Identification | linux | Obsolete (not POSIX compliant) |
|
|
||||||
| Identification | \_\_linux | Obsolete (not POSIX compliant) |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/LynxOS">LynxOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------- |
|
|
||||||
| Identification | **Lynx** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Mac_OS">MacOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | --------------------- | -------------------------------------- |
|
|
||||||
| Identification | macintosh | Mac OS 9 |
|
|
||||||
| Identification | Macintosh | Mac OS 9 |
|
|
||||||
| Identification | **APPLE** && **MACH** | Mac OS XDefined by GNU C and Intel C++ |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/OS-9">Microware OS-9</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ---------- | ------------------------- |
|
|
||||||
| Identification | \_\_OS9000 | Defined by Ultimate C/C++ |
|
|
||||||
| Identification | \_OSK | Defined by Ultimate C/C++ |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Minix">MINIX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | --------- |
|
|
||||||
| Identification | \_\_minix |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Morphos">MorphOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----------- |
|
|
||||||
| Identification | **MORPHOS** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/MPE">MPE/iX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | --------- |
|
|
||||||
| Identification | mpeix |
|
|
||||||
| Identification | \_\_mpexl |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/MS-DOS">MSDOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | --------- |
|
|
||||||
| Identification | MSDOS |
|
|
||||||
| Identification | **MSDOS** |
|
|
||||||
| Identification | \_MSDOS |
|
|
||||||
| Identification | **DOS** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Netbsd">NetBSD</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | ------------------ | ---------- | -------------------------------------------------------------------------------------------------------------------------- |
|
|
||||||
| Identification | **NetBSD** | | |
|
|
||||||
| Version | BSD | | |
|
|
||||||
| Version | NetBSD'V'\_'R' | | V = VersionR = RevisionMust be included from \<sys/param.h\> |
|
|
||||||
| Version | **NetBSD_Version** | VVRRAAPP00 | VV = VersionRR = RevisionAA = ReleasePP = PatchFrom NetBSD 1.2D (?) until NetBSD 2.0HMust be included from \<sys/param.h\> |
|
|
||||||
| Version | **NetBSD_Version** | VVRR00PP00 | VV = VersionRR = RevisionPP = PatchFrom NetBSD 2.99.9Must be included from \<sys/param.h\> |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| NetBSD | **NetBSD_Version** | Macro |
|
|
||||||
| ------ | ------------------ | ------------- |
|
|
||||||
| 0.8 | | NetBSD0_8 |
|
|
||||||
| 0.9 | | NetBSD0_9 |
|
|
||||||
| 1.0 | | NetBSD1_0 = 1 |
|
|
||||||
| 1.0A | | NetBSD1_0 = 2 |
|
|
||||||
| 1.2D | 102040000 | |
|
|
||||||
| 1.2.1 | 102000100 | |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/NonStop">NonStop</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ---------- |
|
|
||||||
| Identification | \_\_TANDEM |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Nucleus_RTOS">Nucleus RTOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----------- |
|
|
||||||
| Identification | **nucleus** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Openbsd">OpenBSD</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | --------------- | ------ | -------------------------------------------------------- |
|
|
||||||
| Identification | **OpenBSD** | | |
|
|
||||||
| Version | BSD | | |
|
|
||||||
| Version | OpenBSD'V'\_'R' | | V = VersionR = RevisionMust be included from sys/param.h |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| OpenBSD | Macro |
|
|
||||||
| ------- | ---------- |
|
|
||||||
| 3.1 | OpenBSD3_1 |
|
|
||||||
| 3.9 | OpenBSD3_9 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/OS/2">OS/2</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----------- |
|
|
||||||
| Identification | OS2 |
|
|
||||||
| Identification | \_OS2 |
|
|
||||||
| Identification | **OS2** |
|
|
||||||
| Identification | **TOS_OS2** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Palmos">Palm OS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ---------- | ----------------------------- |
|
|
||||||
| Identification | **palmos** | Defined by GNU C in PRC-Tools |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Plan_9_from_Bell_Labs">Plan 9</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------ |
|
|
||||||
| Identification | EPLAN9 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/DC/OSx">Pyramid DC/OSx</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----- |
|
|
||||||
| Identification | pyr |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/QNX">QNX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | --------------------- | ---------- | ------------------------------------------------------------------------------------------------------------------------ |
|
|
||||||
| Identification | **QNX** | | QNX 4.x |
|
|
||||||
| Identification | **QNXNTO** | | QNX 6.x |
|
|
||||||
| Version | \_NTO_VERSION | VRR | V = VersionRR = RevisionOnly available when **QNXNTO** is defined.Must be included from sys/neutrino.h/ |
|
|
||||||
| Version | BBNDK_VERSION_CURRENT | VVRRRRPPPP | V = VersionRRRR = RevisionPPPP = PatchOnly available on Blackberry 10From Blackberry 10.1.0Must be included from bbndk.h |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| QNX | \_NTO_VERSION |
|
|
||||||
| --- | ------------- |
|
|
||||||
| 6.2 | 620 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Reliant_UNIX">Reliant UNIX</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----- |
|
|
||||||
| Identification | sinux |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/SCO_OpenServer">SCO OpenServer</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | -------- | ---------------- |
|
|
||||||
| Identification | M_I386 | Defined by GNU C |
|
|
||||||
| Identification | M_XENIX | Defined by GNU C |
|
|
||||||
| Identification | \_SCO_DS | |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Solaris_Operating_Environment">Solaris</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | --------------------- | ----------------------------------------------------------------------------------------------------------- |
|
|
||||||
| Identification | sun | |
|
|
||||||
| Identification | \_\_sun | |
|
|
||||||
| Version | \__'System'_'Version' | System = uname -sVersion = uname -rAny illegal character is replaced by an underscore.Defined by Sun Studio |
|
|
||||||
|
|
||||||
Use the SVR4 macros to distinguish between Solaris and SunOS.
|
|
||||||
#if defined(sun) || defined(**sun) # if defined(**SVR4) || defined(**svr4**) /_ Solaris _/ # else /_ SunOS _/ # endif #endif
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| Solaris | Macro |
|
|
||||||
| ------- | ------------- |
|
|
||||||
| 2.7 | \_\_SunOS_5_7 |
|
|
||||||
| 8 | \_\_SunOS_5_8 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Stratus_VOS">Stratus VOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | ------- | ------ | ----------- |
|
|
||||||
| Identification | **VOS** | | |
|
|
||||||
| Version | **VOS** | V | V = Version |
|
|
||||||
|
|
||||||
Notice that the `__VOS__` macro is defined by the compiler, but as several compilers can co-exist in the same OS release, the version number is not reliable.
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/UNIX_System_V">SVR4 Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | -------------- | --------------- |
|
|
||||||
| Identification | **sysv** | |
|
|
||||||
| Identification | \_\_SVR4 | |
|
|
||||||
| Identification | **svr4** | |
|
|
||||||
| Identification | \_SYSTYPE_SVR4 | Defined on IRIX |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Syllable_Desktop">Syllable</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------------ |
|
|
||||||
| Identification | **SYLLABLE** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Symbian_OS">Symbian OS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------------- |
|
|
||||||
| Identification | **SYMBIAN32** |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Digital_UNIX">Tru64 (OSF/1)</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------- |
|
|
||||||
| Identification | **osf** |
|
|
||||||
| Identification | \_\_osf |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Ultrix">Ultrix</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ---------- |
|
|
||||||
| Identification | ultrix |
|
|
||||||
| Identification | \_\_ultrix |
|
|
||||||
| Identification | **ultrix** |
|
|
||||||
| Identification | unix & vax |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/UNICOS">UNICOS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | -------- | ------ | ----------- |
|
|
||||||
| Identification | \_UNICOS | | |
|
|
||||||
| Version | \_UNICOS | V | V = Version |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Unicos">UNICOS/mp</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ---------------- | ----------- |
|
|
||||||
| Identification | \_CRAY\_\_crayx1 | |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Unix">UNIX Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | -------- |
|
|
||||||
| Identification | **unix** |
|
|
||||||
| Identification | \_\_unix |
|
|
||||||
|
|
||||||
Notice that not all compilers defines these macros, e.g. the xlC or the DEC C/C++ compiler, so it may be better to use the POSIX or X/Open standard macros instead.
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/UnixWare">UnixWare</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ----------- |
|
|
||||||
| Identification | sco |
|
|
||||||
| Identification | \_UNIXWARE7 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/UWIN">U/Win Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro |
|
|
||||||
| -------------- | ------ |
|
|
||||||
| Identification | \_UWIN |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Vms">VMS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | ----------- | --------- | ------------------------------------------------------------------------------------------------ |
|
|
||||||
| Identification | VMS | | |
|
|
||||||
| Identification | \_\_VMS | | |
|
|
||||||
| Version | \_\_VMS_VER | VVRREPPTT | VV = VersionRR = RevisionE = Edit numberPP = Patch (01 = A, ... 26 = Z)TT = Type (22 = official) |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| VMS | \_\_VMS_VER |
|
|
||||||
| ------ | ----------- |
|
|
||||||
| 6.1 | 60100022 |
|
|
||||||
| 6.2 | 60200022 |
|
|
||||||
| 6.2-1I | 60210922 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/VxWorks">VxWorks</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description | |
|
|
||||||
| -------------- | ------------------- | ------------------------------------------------ | --- |
|
|
||||||
| Identification | **VXWORKS** | Defined by GNU C and Diab (from ?) | |
|
|
||||||
| Identification | \_\_vxworks | Defined by GNU C and Diab (from ?) | |
|
|
||||||
| Version | \_WRS_VXWORKS_MAJOR | VersionMust be included from version.h | |
|
|
||||||
| Version | \_WRS_VXWORKS_MINOR | RevisionMust be included from version.h | |
|
|
||||||
| Version | \_WRS_VXWORKS_MAINT | Patch/maintenanceMust be included from version.h | |
|
|
||||||
| Mode | **RTP** | For real-time mode | |
|
|
||||||
| Mode | \_WRS_KERNEL | For kernel mode | |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| VxWorks | \_WRS_VXWORKS_MAJOR | \_WRS_VXWORKS_MINOR | \_WRS_VXWORKS_MAINT |
|
|
||||||
| ------- | ------------------- | ------------------- | ------------------- |
|
|
||||||
| 6.2 | 6 | 2 | 0 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Category:Microsoft_Windows">Windows</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ----------- | ------------------------------------------------- |
|
|
||||||
| Identification | \_WIN16 | Defined for 16-bit environments 1 |
|
|
||||||
| Identification | \_WIN32 | Defined for both 32-bit and 64-bit environments 1 |
|
|
||||||
| Identification | \_WIN64 | Defined for 64-bit environments 1 |
|
|
||||||
| Identification | **WIN32** | Defined by Borland C++ |
|
|
||||||
| Identification | **TOS_WIN** | Defined by xlC |
|
|
||||||
| Identification | **WINDOWS** | Defined by Watcom C/C++ |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Windows_CE">Windows CE</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | ------------------ | ------ | ------------------------------------- |
|
|
||||||
| Identification | \_WIN32_WCE | | Defined by Embedded Visual Studio C++ |
|
|
||||||
| Version | \_WIN32_WCE | VRR | V = VersionR = Revision |
|
|
||||||
| Identification | WIN32*PLATFORM*'P' | | P = Platform |
|
|
||||||
| Version | WIN32*PLATFORM*'P' | V | P = PlatformV = Version |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| Version | \_WIN32_WCE |
|
|
||||||
| ------- | ----------- |
|
|
||||||
| 2.01 | 201 |
|
|
||||||
| 2.11 | 211 |
|
|
||||||
| 3.0 | 300 |
|
|
||||||
| 4.0 | 400 |
|
|
||||||
| 4.1 | 410 |
|
|
||||||
| 4.2 | 420 |
|
|
||||||
| 5.0 | 501 |
|
|
||||||
|
|
||||||
| Platform | Macro | Value |
|
|
||||||
| ------------------- | ---------------------- | ----- |
|
|
||||||
| H/PC 2000 | WIN32_PLATFORM_HPC2000 | |
|
|
||||||
| H/PC Pro 2.11 | WIN32_PLATFORM_HPCPRO | 211 |
|
|
||||||
| H/PC Pro 3.0 | WIN32_PLATFORM_HPCPRO | 300 |
|
|
||||||
| Pocket PC | WIN32_PLATFORM_PSPC | 1 |
|
|
||||||
| Pocket PC 2002 | WIN32_PLATFORM_PSPC | 310 |
|
|
||||||
| Windows Mobile 2003 | WIN32_PLATFORM_PSPC | 400 |
|
|
||||||
| Smartphone 2002 | WIN32_PLATFORM_WFSP | 100 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Bristol_Technology_Inc.">Wind/U Environment</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Format | Description |
|
|
||||||
| -------------- | -------------- | -------- | ----------------------------------- |
|
|
||||||
| Identification | \_WINDU_SOURCE | | |
|
|
||||||
| Version | \_WINDU_SOURCE | 0xVVRRPP | VV = VersionRR = RevisionPP = Patch |
|
|
||||||
|
|
||||||
**Example**
|
|
||||||
|
|
||||||
| Wind/U | \_WINDU_SOURCE |
|
|
||||||
| ------ | -------------- |
|
|
||||||
| 3.1.2 | 0x030102 |
|
|
||||||
|
|
||||||
**<u><a rel="nofollow noreferrer" class="wrap external" href="http://en.wikipedia.org/wiki/Z/OS">z/OS</a></u>**
|
|
||||||
|
|
||||||
| Type | Macro | Description |
|
|
||||||
| -------------- | ----------- | ----------- |
|
|
||||||
| Identification | **MVS** | Host |
|
|
||||||
| Identification | **HOS_MVS** | Host |
|
|
||||||
| Identification | **TOS_MVS** | Target |
|
|
||||||
@@ -1,346 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Use differential equation method and matrix method to find Fibonacci sequence general formula"
|
|
||||||
time: "2023-11-20"
|
|
||||||
tags: ["mathematics"]
|
|
||||||
pin: true
|
|
||||||
summary: "This article gives two methods to derive Fibonacci sequence: matrix method and difference equation method"
|
|
||||||
---
|
|
||||||
|
|
||||||
Here is the translation of the provided article into English:
|
|
||||||
|
|
||||||
In Fibonacci's work _The Book of Calculation_ the Fibonacci sequence is defined as follows:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = \begin{cases}
|
|
||||||
0 & \text{if } n = 0 \\
|
|
||||||
1 & \text{if } n = 1 \\
|
|
||||||
F_{n-1} + F_{n-2} & \text{if } n \geq 2
|
|
||||||
\end{cases}
|
|
||||||
$$
|
|
||||||
|
|
||||||
It can be proven that its closed-form formula is:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n\right)
|
|
||||||
$$
|
|
||||||
|
|
||||||
With my current knowledge, I can only comprehend two proof methods as follows:
|
|
||||||
|
|
||||||
## Matrix Method
|
|
||||||
|
|
||||||
Let's first discuss the case when $n \geq 2$. Our goal now is to transform the recurrence formula of the Fibonacci sequence into matrix form. How can we do that? We can approach it from the perspective of a system of linear equations.
|
|
||||||
|
|
||||||
First, here is what we know:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_{n-1} + F_{n-2} = F_{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
We can add the equation $F_{n-1} + 0 \cdot F_{n-2} = F_{n-1}$ to form a system of linear equations:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{cases}
|
|
||||||
F_{n-1} + F_{n-2} = F_{n} \\
|
|
||||||
F_{n-1} + 0 \cdot F_{n-2} = F_{n-1}
|
|
||||||
\end{cases}
|
|
||||||
$$
|
|
||||||
|
|
||||||
This can be transformed into matrix form as follows:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{bmatrix}
|
|
||||||
1 & 1 \\
|
|
||||||
1 & 0
|
|
||||||
\end{bmatrix}
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{n-1} \\
|
|
||||||
F_{n-2}
|
|
||||||
\end{bmatrix}
|
|
||||||
=
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{n} \\
|
|
||||||
F_{n-1}
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Now, we can iterate this process:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{align}
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{n} \\
|
|
||||||
F_{n-1}
|
|
||||||
\end{bmatrix}
|
|
||||||
&=
|
|
||||||
\begin{bmatrix}
|
|
||||||
1 & 1 \\
|
|
||||||
1 & 0
|
|
||||||
\end{bmatrix}
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{n-1} \\
|
|
||||||
F_{n-2}
|
|
||||||
\end{bmatrix} \\
|
|
||||||
&=
|
|
||||||
\begin{bmatrix}
|
|
||||||
1 & 1 \\
|
|
||||||
1 & 0
|
|
||||||
\end{bmatrix}^2
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{n-2} \\
|
|
||||||
F_{n-3}
|
|
||||||
\end{bmatrix} \\
|
|
||||||
&=\cdots \\
|
|
||||||
&=
|
|
||||||
\begin{bmatrix}
|
|
||||||
1 & 1 \\
|
|
||||||
1 & 0
|
|
||||||
\end{bmatrix}^{n-1}
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{1} \\
|
|
||||||
F_{0}
|
|
||||||
\end{bmatrix}
|
|
||||||
\end{align}
|
|
||||||
$$
|
|
||||||
|
|
||||||
We denote the matrix $\boldsymbol{A} = \begin{bmatrix}
|
|
||||||
1 & 1 \\
|
|
||||||
1 & 0
|
|
||||||
\end{bmatrix}$. So, the problem becomes finding $\boldsymbol{A}^{n-1}$, and then we can calculate $\boldsymbol{A}^{n}$ and replace all instances of $n$ with $n-1$.
|
|
||||||
|
|
||||||
Notice that matrix $\boldsymbol{A}$ is a square matrix, and we can utilize the eigenvalues and eigenvectors of matrices.
|
|
||||||
|
|
||||||
Eigenvectors can be understood as vectors that, when right-multiplied by the matrix, result in a vector parallel to themselves. Eigenvalues are the scaling factors by which the eigenvectors are scaled when right-multiplied by the matrix. In other words:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{A}\boldsymbol{x} = \lambda\boldsymbol{x}\tag{1}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Here, $\lambda$ is the eigenvalue, and the non-zero vector $\boldsymbol{x} \in \mathbb{R}^n$ (where $n$ is the order of the square matrix) is the eigenvector corresponding to the eigenvalue $\lambda$ of matrix $\boldsymbol{A}$.
|
|
||||||
|
|
||||||
So, the specific approach is to first find the eigenvalues $\lambda_1$ and $\lambda_2$ (usually, an $n$-order matrix has $n$ eigenvalues) and obtain the diagonal matrix $\rm{diag}\{\lambda_1, \lambda_2\}$. Then, we find an invertible matrix $\boldsymbol{P}$ such that:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P} = \rm{diag}\{\lambda_1, \lambda_2\}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Using matrix multiplication properties:
|
|
||||||
|
|
||||||
$$
|
|
||||||
(\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P})^n = \boldsymbol{P}^{-1}\boldsymbol{A}(\boldsymbol{P}\boldsymbol{P}^{-1})\boldsymbol{A}(\boldsymbol{P}\cdots\boldsymbol{P}^{-1})\boldsymbol{A}\boldsymbol{P} = \boldsymbol{P}^{-1}\boldsymbol{A}^n\boldsymbol{P}\tag{2}
|
|
||||||
$$
|
|
||||||
|
|
||||||
This allows us to calculate $\boldsymbol{A}^{n}$.
|
|
||||||
|
|
||||||
Let's first find the eigenvalues. We can rewrite equation $(1)$ as:
|
|
||||||
|
|
||||||
$$
|
|
||||||
(\boldsymbol{A}-\lambda\boldsymbol{E})\boldsymbol{x} = \boldsymbol{0}\tag{3}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Here, $\boldsymbol{E}$ is the identity matrix, and we can compute that $\boldsymbol{A}-\lambda\boldsymbol{E} = \begin{bmatrix}
|
|
||||||
1-\lambda & 1 \\
|
|
||||||
1 & -\lambda
|
|
||||||
\end{bmatrix}$. To ensure that there is a non-zero solution, we solve for:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| \boldsymbol{A}-\lambda\boldsymbol{E} \right| = \begin{vmatrix}
|
|
||||||
1-\lambda & 1 \\
|
|
||||||
1 & -\lambda
|
|
||||||
\end{vmatrix} = \lambda^2 - \lambda - 1 = 0
|
|
||||||
$$
|
|
||||||
|
|
||||||
Solving this equation, we obtain $\lambda_1 = \frac{1+\sqrt{5}}{2}$ and $\lambda_2 = \frac{1-\sqrt{5}}{2}$.
|
|
||||||
|
|
||||||
Therefore, the diagonal matrix is:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\rm{diag}\{\lambda_1, \lambda_2\} = \begin{bmatrix}
|
|
||||||
\frac{1+\sqrt{5}}{2} & 0 \\
|
|
||||||
0 & \frac{1-\sqrt{5}}{2}
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Assuming the eigenvector is $\boldsymbol{x} = \begin{bmatrix}
|
|
||||||
x & y
|
|
||||||
\end{bmatrix}^T$, we can substitute $\lambda_1$ and $\lambda_2$ into equation $(2)$ to obtain two systems of equations:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{cases}
|
|
||||||
(1-\lambda_1)x + y = 0 \\
|
|
||||||
x - \lambda_1y = 0
|
|
||||||
\end{cases},
|
|
||||||
\begin{cases}
|
|
||||||
(1-\lambda_2)x + y = 0 \\
|
|
||||||
x - \lambda_2y = 0
|
|
||||||
\end{cases}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Setting $y = 1$ in both systems of equations gives us the two eigenvectors of the matrix:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{x}_1 = \begin{bmatrix}
|
|
||||||
\frac{1+\sqrt{5}}{2} & 1
|
|
||||||
\end{bmatrix}^T,
|
|
||||||
\boldsymbol{x}_2 = \begin{bmatrix}
|
|
||||||
\frac{1-\sqrt{5}}{2} & 1
|
|
||||||
\end{bmatrix}^T
|
|
||||||
$$
|
|
||||||
|
|
||||||
So, the invertible matrix $\boldsymbol{P}$ is formed by these two eigenvectors:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{P} = \begin{bmatrix}
|
|
||||||
\frac{1+\sqrt{5}}{2} & \frac{1-\sqrt{5}}{2} \\
|
|
||||||
1 & 1
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Why is it like this? Let $\boldsymbol{P} = \begin{bmatrix}
|
|
||||||
x_1 & x_2 \\
|
|
||||||
y_1 & y_2
|
|
||||||
\end{bmatrix}$ (where $x_1, y_1, x_2, y_2$ are the components of eigenvectors $\boldsymbol{x}_1, \boldsymbol{x}_2$ respectively).
|
|
||||||
|
|
||||||
Now, if we calculate $\boldsymbol{P}\rm{diag}\{\lambda_1, \lambda_2\}$, it exactly equals $\begin{bmatrix}
|
|
||||||
\lambda_1x_1 & \lambda_2x_2 \\
|
|
||||||
\lambda_1y_1 & \lambda_2y_2
|
|
||||||
\end{bmatrix}$. This means that $\boldsymbol{A}\boldsymbol{P} = \boldsymbol{P}\rm{diag}\{\lambda_1, \lambda_2\}$ is inevitable. Left-multiplying by $\boldsymbol{P}^{-1}$, we get $\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P} = \rm{diag}\{\lambda_1, \lambda_2\}$. So, $\boldsymbol{P} = \begin{bmatrix}
|
|
||||||
x_1 & x_2 \\
|
|
||||||
y_1 & y_2
|
|
||||||
\end{bmatrix}$ is reasonable.
|
|
||||||
|
|
||||||
Its inverse matrix is easy to calculate:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{P}^{-1} = \frac{\boldsymbol{P}^*}{\left|\boldsymbol{P}\right|} = \frac{1}{\sqrt{5}}\begin{bmatrix}
|
|
||||||
1 & \frac{1-\sqrt{5}}{2} \\
|
|
||||||
1 & \frac{1+\sqrt{5}}{2}
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Substituting into equation $(2)$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{A}^n = \boldsymbol{P}(\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P})^n\boldsymbol{P}^{-1} = \boldsymbol{P}\rm{diag}^n\{\lambda_1, \lambda_2\}\boldsymbol{P}^{-1}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Where the diagonal matrix is:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\rm{diag}^n\{\lambda_1, \lambda_2\} = \begin{bmatrix}
|
|
||||||
\left(\frac{1+\sqrt{5}}{2}\right)^n & 0 \\
|
|
||||||
0 & \left(\frac{1-\sqrt{5}}{2}\right)^n
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Therefore,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\boldsymbol{A}^n = \frac{1}{\sqrt{5}}\begin{bmatrix}
|
|
||||||
\left(\frac{1+\sqrt{5}}{2}\right)^{n+1} + \left(\frac{1-\sqrt{5}}{2}\right)^{n+1} & \left(\frac{1+\sqrt{5}}{2}\right)^{n+1}\left(\frac{1-\sqrt{5}}{2}\right) + \left(\frac{1-\sqrt{5}}{2}\right)^{n+1}\left(\frac{1+\sqrt{5}}{2}\right) \\
|
|
||||||
\left(\frac{1+\sqrt{5}}{2}\right)^n + \left(\frac{1-\sqrt{5}}{2}\right)^n & \left(\frac{1+\sqrt{5}}{2}\right)^{n}\left(\frac{1-\sqrt{5}}{2}\right) + \left(\frac{1-\sqrt{5}}{2}\right)^{n}\left(\frac{1+\sqrt{5}}{2}\right)
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Then,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_{n} \\
|
|
||||||
F_{n-1}
|
|
||||||
\end{bmatrix}
|
|
||||||
= \boldsymbol{A}^{n-1}
|
|
||||||
\begin{bmatrix}
|
|
||||||
F_1 \\
|
|
||||||
F_0
|
|
||||||
\end{bmatrix}
|
|
||||||
= \frac{1}{\sqrt{5}}\begin{bmatrix}
|
|
||||||
\left(\frac{1+\sqrt{5}}{2}\right)^{n} + \left(\frac{1-\sqrt{5}}{2}\right)^{n} \\
|
|
||||||
\left(\frac{1+\sqrt{5}}{2}\right)^{n-1} + \left(\frac{1-\sqrt{5}}{2}\right)^{n-1}
|
|
||||||
\end{bmatrix}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Considering only the first row of the matrices on both sides of the equation, we obtain the closed-form formula for the Fibonacci sequence:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n\right)
|
|
||||||
$$
|
|
||||||
|
|
||||||
Substituting $n=0$ and $n=1$ to verify, we find that they both satisfy the equation.
|
|
||||||
|
|
||||||
---
|
|
||||||
|
|
||||||
## Difference Equation Method
|
|
||||||
|
|
||||||
Defining the difference of a sequence $\{a_n\}$ as $\Delta a_n = a_{n+1} - a_n$ (using backward difference here), we can define the second-order difference as:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\Delta^2 a_n = \Delta a_{n+1} - \Delta a_n = a_{n+2} - 2a_{n+1} + a_n
|
|
||||||
$$
|
|
||||||
|
|
||||||
Further, we can define the $m$-th order difference:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\Delta^m a_n = \Delta^{m-1} a_{n+1} - \Delta^{m-1} a_n = \sum_{i=0}^{m} (-1)^i C_m^i a_{n+m-i}
|
|
||||||
$$
|
|
||||||
|
|
||||||
And
|
|
||||||
|
|
||||||
$$
|
|
||||||
F(a_n, \Delta a_n,
|
|
||||||
\Delta a_n, \Delta^2 a_n, \Delta^3 a_n, \ldots)
|
|
||||||
$$
|
|
||||||
|
|
||||||
The Fibonacci sequence, defined as $F_n = F_{n-1} + F_{n-2}$, has a second-order difference that is constant:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\Delta^2 F_n = F_{n+2} - 2F_{n+1} + F_n = F_{n+1} + F_{n+1} - 2F_{n+1} + F_n = F_{n+1} - F_n = F_n
|
|
||||||
$$
|
|
||||||
|
|
||||||
Now, we can write the second-order linear homogeneous difference equation for $F_n$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\Delta^2 F_n - F_n = 0
|
|
||||||
$$
|
|
||||||
|
|
||||||
This is a characteristic equation, and we can solve it by assuming $F_n = r^n$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
r^2 - 1 = 0
|
|
||||||
$$
|
|
||||||
|
|
||||||
Solving this equation gives us two solutions: $r = 1$ and $r = -1$. Therefore, the general solution for the homogeneous difference equation is:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = c_1 \cdot 1^n + c_2 \cdot (-1)^n
|
|
||||||
$$
|
|
||||||
|
|
||||||
Now, we need initial conditions to find the particular solution. We know that $F_0 = 0$ and $F_1 = 1$. Substituting these into the general solution:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{align*}
|
|
||||||
F_0 &= c_1 \cdot 1^0 + c_2 \cdot (-1)^0 = c_1 + c_2 = 0 \\
|
|
||||||
F_1 &= c_1 \cdot 1^1 + c_2 \cdot (-1)^1 = c_1 - c_2 = 1
|
|
||||||
\end{align*}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Solving this system of equations, we find $c_1 = \frac{1}{2}$ and $c_2 = -\frac{1}{2}$. Therefore, the particular solution for the Fibonacci sequence is:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = \frac{1}{2} \cdot 1^n - \frac{1}{2} \cdot (-1)^n
|
|
||||||
$$
|
|
||||||
|
|
||||||
This can be simplified further by noting that $(-1)^n$ is equal to $(-1)^{n-1} \cdot (-1) = -(-1)^{n-1}$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = \frac{1}{2} - \frac{1}{2} \cdot (-1)^{n-1}
|
|
||||||
$$
|
|
||||||
|
|
||||||
This is indeed the closed-form formula for the Fibonacci sequence:
|
|
||||||
|
|
||||||
$$
|
|
||||||
F_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n\right)
|
|
||||||
$$
|
|
||||||
|
|
||||||
So, we have successfully derived the same result using the difference equation method.
|
|
||||||
|
|
||||||
In summary, both the matrix method and the difference equation method lead to the same closed-form expression for the Fibonacci sequence, demonstrating the beauty of mathematics in providing multiple ways to arrive at a solution.
|
|
||||||
@@ -1,65 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Joseph Circle Problem"
|
|
||||||
time: "2023-11-21"
|
|
||||||
tags: ["algorithm"]
|
|
||||||
summary: "A description, analysis and solution for joseph circle problem."
|
|
||||||
---
|
|
||||||
|
|
||||||
## Problem Description
|
|
||||||
|
|
||||||
The Josephus problem is a classic mathematical problem that describes the following scenario:
|
|
||||||
|
|
||||||
There are $n$ people standing in a circle. Starting from a certain person, they count off in sequence, and every $m$-th person steps out of the circle. The counting and elimination process continues, looping back to the next person when the end of the circle is reached. This continues until only one person remains. The problem is to determine the initial position of the last person remaining in the circle.
|
|
||||||
|
|
||||||
For example, when $n=7$ and $m=3$, the order of elimination is: $3, 6, 2, 7, 5, 1$. The last person remaining is at position $4$.
|
|
||||||
|
|
||||||
## Solution
|
|
||||||
|
|
||||||
The Josephus problem can be solved using either recursion or mathematical formulas. The recursive solution assumes knowledge of the solution for $n-1$ people, denoted as $f(n-1, m)$, and then calculates the solution for $n$ people using the formula:
|
|
||||||
|
|
||||||
$
|
|
||||||
f(n, m) = (f(n-1, m) + m) \% n
|
|
||||||
$
|
|
||||||
|
|
||||||
Here, $\%$ denotes the modulo operation. The base case is $f(1, m) = 0$, representing the solution when there is only one person.
|
|
||||||
|
|
||||||
The mathematical formula solution is derived based on the recurrence relation, resulting in the same formula:
|
|
||||||
|
|
||||||
$
|
|
||||||
f(n, m) = (f(n-1, m) + m) \% n
|
|
||||||
$
|
|
||||||
|
|
||||||
## Programming Implementation
|
|
||||||
|
|
||||||
When it comes to solving the Josephus problem, dynamic programming is an effective approach. Here is an example C code implementing dynamic programming to solve the Josephus problem:
|
|
||||||
|
|
||||||
```c
|
|
||||||
#include <stdio.h>
|
|
||||||
|
|
||||||
int josephus(int n, int m) {
|
|
||||||
int dp[n + 1];
|
|
||||||
dp[1] = 0; // Initial position when there is only one person
|
|
||||||
|
|
||||||
for (int i = 2; i <= n; i++) {
|
|
||||||
dp[i] = (dp[i - 1] + m) % i;
|
|
||||||
}
|
|
||||||
|
|
||||||
return dp[n];
|
|
||||||
}
|
|
||||||
|
|
||||||
int main() {
|
|
||||||
int n = 7; // Total number of people
|
|
||||||
int m = 3; // Count off to m for elimination
|
|
||||||
|
|
||||||
int lastPerson = josephus(n, m);
|
|
||||||
printf("The last person remaining is: %d\n", lastPerson + 1); // Adding 1 due to 0-based indexing
|
|
||||||
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
In the above code, we use a dynamic programming array `dp` to store the next position after each person is eliminated. Through iteration, we can find the initial position of the last person remaining in the circle. In the `main` function, we set the total number of people `n` and the count to `m` for elimination. Then, we call the `josephus` function to calculate the position of the last person remaining and print the result.
|
|
||||||
|
|
||||||
Note that we assume people's positions start from 1, while array indices start from 0. Therefore, when printing the position of the last person remaining, we need to add 1.
|
|
||||||
|
|
||||||
Using dynamic programming provides an efficient solution to the Josephus problem, avoiding the repetitive calculations of recursion and improving code performance.
|
|
||||||
@@ -1,123 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Rabin-Karp Algorithm"
|
|
||||||
time: "2023-11-22"
|
|
||||||
tags: ["algorithm"]
|
|
||||||
summary: "It is designed to address the multiple pattern string matching problem."
|
|
||||||
---
|
|
||||||
|
|
||||||
The Rabin-Karp algorithm, also known as the Karp-Rabin algorithm, was introduced by _Richard M. Karp_ and _Michael O. Rabin_ in 1987. It is designed to address the multiple pattern string matching problem.
|
|
||||||
|
|
||||||
Its implementation is somewhat unconventional. It begins by computing the hash values of two strings and then determines whether there is a match by comparing these hash values.
|
|
||||||
|
|
||||||
## Algorithm Analysis and Implementation
|
|
||||||
|
|
||||||
Choosing an appropriate hash function is crucial. Assuming the text string is $t[0, n)$, and the pattern string is $p[0, m)$, where $0<m<n$, let $Hash(t[i,j])$ represent the hash value of the substring $t[i, j]$.
|
|
||||||
|
|
||||||
When $Hash(t[0, m-1])!=Hash(p[0,m-1])$, it is natural to compare $Hash(t[1, m])$. In this process, if we recalculate the hash value for the substring $t[1, m]$, it would require $O(n)$ time complexity, which is not cost-effective. Observing that there are m-1 overlapping characters between the substrings $t[0, m-1]$ and $t[1, m]$, we can use a rolling hash function. This reduces the time complexity of recalculation to $O(1)$.
|
|
||||||
|
|
||||||
The rolling hash function used in the Rabin-Karp algorithm primarily leverages the concept of [Rabin fingerprint](https://en.wikipedia.org/wiki/Rabin_fingerprint). For example, the formula to calculate the hash value of the substring $t[0, m-1]$ is as follows:
|
|
||||||
|
|
||||||
$$
|
|
||||||
Hash(t[0, m-1])=t[0]*b^{m-1}+t[1]*b^{m-2}+...+t[m-1]*b^0
|
|
||||||
\\
|
|
||||||
\tag{t[0] represents the ASCII code of the character}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Here, $b$ is a constant. In Rabin-Karp, it is generally set to 256 because the maximum value of a character does not exceed 255. The formula above has an issue - hash values could overflow. To address this, we take the modulus, and the value should be as large as possible and preferably a prime number. Here, we take 101.
|
|
||||||
|
|
||||||
The formula to calculate the hash value of the substring $t[1, m]$ is then:
|
|
||||||
|
|
||||||
$$
|
|
||||||
Hash(t[1,m])=(Hash(t[0,m-1])-t[0]*b^{m-1})*b+t[m]*b^0\\\tag{Please compare with the previous formula}
|
|
||||||
$$
|
|
||||||
|
|
||||||
The complete code is as follows:
|
|
||||||
|
|
||||||
```cpp
|
|
||||||
#include <iostream>
|
|
||||||
#include <string.h>
|
|
||||||
|
|
||||||
using namespace std;
|
|
||||||
|
|
||||||
#define BASE 256
|
|
||||||
#define MODULUS 101
|
|
||||||
|
|
||||||
void RabinKarp(char t[], char p[])
|
|
||||||
{
|
|
||||||
int t_len = strlen(t);
|
|
||||||
int p_len = strlen(p);
|
|
||||||
|
|
||||||
// For rolling hash
|
|
||||||
int h = 1;
|
|
||||||
for (int i = 0; i < p_len - 1; i++)
|
|
||||||
h = (h * BASE) % MODULUS;
|
|
||||||
|
|
||||||
int t_hash = 0;
|
|
||||||
int p_hash = 0;
|
|
||||||
for (int i = 0; i < p_len; i++)
|
|
||||||
{
|
|
||||||
t_hash = (BASE * t_hash + t[i]) % MODULUS;
|
|
||||||
p_hash = (BASE * p_hash + p[i]) % MODULUS;
|
|
||||||
}
|
|
||||||
|
|
||||||
int i = 0;
|
|
||||||
while (i <= t_len - p_len)
|
|
||||||
{
|
|
||||||
// Considering the possibility of hash collisions, we use memcmp for additional verification
|
|
||||||
if (t_hash == p_hash && memcmp(p, t + i, p_len) == 0)
|
|
||||||
cout << p << " is found at index " << i << endl;
|
|
||||||
|
|
||||||
// Rolling hash
|
|
||||||
t_hash = (BASE * (t_hash - t[i] * h) + t[i + p_len]) % MODULUS;
|
|
||||||
|
|
||||||
// Avoiding negative values
|
|
||||||
if (t_hash < 0)
|
|
||||||
t_hash = t_hash + MODULUS;
|
|
||||||
|
|
||||||
i++;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
int main()
|
|
||||||
{
|
|
||||||
char t[100] = "It is a test, but not just a test";
|
|
||||||
char p[10] = "test";
|
|
||||||
|
|
||||||
RabinKarp(t, p);
|
|
||||||
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
The output is as follows:
|
|
||||||
|
|
||||||
```text
|
|
||||||
test is found at index 8
|
|
||||||
test is found at index 29
|
|
||||||
```
|
|
||||||
|
|
||||||
## Complexity Analysis
|
|
||||||
|
|
||||||
Let's examine the space complexity first, which is easily determined: $S(n)=O(1)$.
|
|
||||||
|
|
||||||
Now, consider the time complexity. Let the length of the text string be n and the pattern string be m. Preprocessing requires $O(m)$, and during matching, in the best case where there are no hash collisions, $T_{best}(n)=O(n-m)$. In the worst case, where there is a collision every time, $T_{worst}(n)=O((n-m)*m)$. In practical scenarios, n is often much larger than m, so the final complexity table is:
|
|
||||||
|
|
||||||
| $S_{n}$ | $O(1)$ |
|
|
||||||
| -------------- | ------- |
|
|
||||||
| $T_{best}(n)$ | $O(n)$ |
|
|
||||||
| $T_{worst}(n)$ | $O(mn)$ |
|
|
||||||
|
|
||||||
## Application Analysis
|
|
||||||
|
|
||||||
The primary application of the Rabin-Karp algorithm is in plagiarism detection for articles, such as the detection system used by [Semantic Scholar](https://www.semanticscholar.org/).
|
|
||||||
|
|
||||||
However, from the complexity data above, the Rabin-Karp algorithm does not seem to have a significant advantage. Is it practical for detecting text plagiarism? Feedback from actual usage results indicates that the time complexity for plagiarism detection is only $O(n)$. I believe this is mainly due to the following two points:
|
|
||||||
|
|
||||||
1. In real-life articles, the text data does not often exhibit as many hash collisions as we might imagine.
|
|
||||||
2. The original content in a submitted article is likely to be much larger than the plagiarized content. In other words, successful matches do not occur as frequently as we might imagine.
|
|
||||||
|
|
||||||
## References
|
|
||||||
|
|
||||||
- [Rabin–Karp algorithm](https://en.wikipedia.org/wiki/Rabin–Karp_algorithm)
|
|
||||||
- [Searching for Patterns | Set 3 (Rabin-Karp Algorithm)](https://www.geeksforgeeks.org/searching-for-patterns-set-3-rabin-karp-algorithm/)
|
|
||||||
- [Computer Algorithms: Rabin-Karp String Searching](http://www.stoimen.com/blog/2012/04/02/computer-algorithms-rabin-karp-string-searching/)
|
|
||||||
@@ -1,195 +0,0 @@
|
|||||||
---
|
|
||||||
title: "The Liskov Substitution Principle"
|
|
||||||
subtitle: ""
|
|
||||||
summary: "A detailed explanation of the Liskov Substitution Principle, What it is, How to use it and why it benefits the architecture of our code."
|
|
||||||
coverURL: null
|
|
||||||
time: "2023-11-28"
|
|
||||||
tags: ["project-practice"]
|
|
||||||
noPrompt: false
|
|
||||||
pin: false
|
|
||||||
---
|
|
||||||
|
|
||||||
## Introduction
|
|
||||||
|
|
||||||
From all the SOLID principles the [Liskov substitution](https://en.wikipedia.org/wiki/Liskov_substitution_principle) principle is the one where the consequences of its violation will become apparent much later in the project. With the violation of any of the other SOLID principles, we can see the problems that can be created almost immediately. A violation of the LSP, will create problems in the future and actually is a late violation of the [Open Closed Principle](https://giannisakritidis.com/blog/The-Open-Closed-Principle/).
|
|
||||||
|
|
||||||
Barbara Liskov in 1988 wrote:
|
|
||||||
|
|
||||||
> What is wanted here is something like the following substitution property: If for each object O1 of type S there is an object O2 of type T such that for all programs P defined in terms of T, the behavior of P is unchanged when O1 is substituted for O2 then S is a subtype of T.`
|
|
||||||
|
|
||||||
The best way to understand the above, is to see examples that violate the LSP and the consequences that this violation will have, but before that, let's see what is a type, what is a subtype, how a subtype is connected to its base type and how those are represented in OOP and more specifically in C#.
|
|
||||||
|
|
||||||
## Types and Subtypes
|
|
||||||
|
|
||||||
Let's say that I have two numbers: `3` and `2`.
|
|
||||||
|
|
||||||
If I say that these numbers are of type `int` then we know that the operation `3/2` will result in `1` and the operation `3+2` wil have a result of `5`.
|
|
||||||
|
|
||||||
If I say that these numbers are of type `float` then the operation `3/2` will have a result of `1.5` and if I say that they are of type `string` then the operation `3+2` will give a result of `32`.
|
|
||||||
|
|
||||||
From the above, we can understand that a type for an outside observer is actually defined by its behaviours. The data it has, is irrelevant for its definition.
|
|
||||||
|
|
||||||
The LSP describes when a type `S` is actually a subtype of `T`, but it is much easier to find out when the `S` is not a subtype of `T` by looking if the LSP is violated.
|
|
||||||
|
|
||||||
## IS A and HAS A Relationships
|
|
||||||
|
|
||||||
In OOP and in C# in particular, we create types and their subtypes with the mechanism of inheritance. Usually we describe inheritance like an `IS A` relationship and composition like a `HAS A` relationship.
|
|
||||||
|
|
||||||
This is not always correct. Although many times an `IS A` relationship can be represented with inheritance, there are times that this will violate the LSP. An `IS A` relationship does not always mean that we should create a base and a child class.
|
|
||||||
|
|
||||||
Before we get to the code examples, let's see why this is true with a real world example.
|
|
||||||
|
|
||||||
When we create a class, for example the class airplane, is this class actually an airplane? The answer is of course no. The class airplane is a piece of code that represents an airplane.
|
|
||||||
|
|
||||||
The problem with real world objects and their representations in code is that the relationships between two objects don't always transfer as relationships between their representatives.
|
|
||||||
|
|
||||||
If I am angry with my neighbor because I think he is making too much noise and he is angry with me because he says that I complain without any real reason and we hire lawyers, our lawyers represent us, their behaviour in court will reflect our opinions and beliefs, but our lawyers are not angry at each other. The angry relationship between myself and my neighbor does not transfer as a relationship between our representatives.
|
|
||||||
|
|
||||||
The same is true for any code we write. For example, a rectangular is a two dimensional shape in the real world and for that reason has width and height. The same is true for a square. As a two dimensional object it has width and height. There is also a relationship between those two shapes. A square `IS A` rectangle that its height equals its width.
|
|
||||||
|
|
||||||
When we create their representations in code, the classes square and rectangle, we might be tempted to make the square class a child of the Rectangle class. After all, in the real world the `IS A` relationship is true, but this will create problems because it is an LSP violation.
|
|
||||||
|
|
||||||
In code, we can represent a square with only one piece of data. A variable called side. This can happen, because square as a type has a condition that is always true, regardless of its state: Its height equals its width. This condition is called invariant and allows us to calculate both the width and the height of the square if we know its side. Although a real world square has width and height, its representation in code doesn't need to.
|
|
||||||
|
|
||||||
If we make the square class, a child of the rectangle class, it will inherit the behaviours of the rectangle class. Specifically the methods that set the width and the height and this will create big problems in the long run. Let's see why.
|
|
||||||
|
|
||||||
## The Square and Rectangle example
|
|
||||||
|
|
||||||
Let's create a rectangle class that has width and height and methods that set and get those values. I don't use properties here, to make the example more clear as properties are actually syntactic sugar in C# for getters and setters.
|
|
||||||
|
|
||||||
```java
|
|
||||||
public class Rectangle
|
|
||||||
{
|
|
||||||
protected float Height;
|
|
||||||
protected float Width;
|
|
||||||
|
|
||||||
public virtual void SetHeight(float height) => Height = height;
|
|
||||||
|
|
||||||
public virtual void SetWidth(float width) => Width = width;
|
|
||||||
|
|
||||||
public float GetHeight() => Height;
|
|
||||||
|
|
||||||
public float GetWidth() => Width;
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
Let's also create the Square class as a child of the rectangle class. To avoid the problem of the square having different height and width, I will set both of those whenever one of them is set.
|
|
||||||
|
|
||||||
```java
|
|
||||||
public class Square : Rectangle
|
|
||||||
{
|
|
||||||
public override void SetHeight(float height)
|
|
||||||
{
|
|
||||||
base.SetHeight(height);
|
|
||||||
Width = height;
|
|
||||||
}
|
|
||||||
|
|
||||||
public override void SetWidth(float width)
|
|
||||||
{
|
|
||||||
base.SetWidth(width);
|
|
||||||
Height = width;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
This might seem that solves any problem we might have. Now our square will always have its width equal to its height. Let's suppose that these classes represent boards that the player character has in a game and is using them to build a fence. So the following code behaves as expected:
|
|
||||||
|
|
||||||
```java
|
|
||||||
Rectangle board = new Rectangle();
|
|
||||||
board.SetWidth(2);
|
|
||||||
board.SetHeight(6);
|
|
||||||
|
|
||||||
Square board2 = new Square();
|
|
||||||
board2.SetWidth(2);
|
|
||||||
board2.SetHeight(6);
|
|
||||||
```
|
|
||||||
|
|
||||||
Our first board will have a width of 2 units and a height of 6 units. Our second board will have both width and height at 6 units, so it will remain a square.
|
|
||||||
|
|
||||||
After some time, let's say six months or so, we get a new requirement: We need a way to show the player how much area his fence will cover.
|
|
||||||
|
|
||||||
That's easy, we create a class that calculates the areas of different shapes. Among the methods of this class, there is a method that calculates the rectangle area that represents the board area, then we can multiply that number with the number of boards the player will use to calculate the fence area.
|
|
||||||
|
|
||||||
Here is the method that will calculate the board area:
|
|
||||||
|
|
||||||
```java
|
|
||||||
public class AreaMethods
|
|
||||||
{
|
|
||||||
public float BoardArea(Rectangle rectangle) => rectangle.GetWidth() * rectangle.GetHeight();
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
This also works fine. The method will calculate the area correctly for both rectangular and square boards.
|
|
||||||
|
|
||||||
After some more time, a new requirement is created. It would be nice to let the player know, how much area his fence would cover if he could lower its height. That's also easy, if for example the player would like his fence to be half the height it was then we, or the programmer responsible for this task can do:
|
|
||||||
|
|
||||||
```java
|
|
||||||
board.SetHeight(board.GetHeight()/2);
|
|
||||||
areaCalculator.BoardArea(board)
|
|
||||||
```
|
|
||||||
|
|
||||||
But this is a bug. What would actually happen is that if the board is a rectangle, then the calculation would be correct, each board would be the same width and half the height, but if the board is of type square, by decreasing its height we also decrease its width. This would calculate the area of a fence that not only is half the height of the previous fence, but also is half the width.
|
|
||||||
|
|
||||||
Will we remember how we have coded the rectangle and square classes after a year or so? Even worse, what if the programmer responsible for that calculation is not us but someone else, what will he do? He would have to go find and check the square implementation so that he can understand why the area calculated, sometimes is half of what the correct result should be.
|
|
||||||
|
|
||||||
The reason we found ourselves in this situation, is because the child class (the square) has a different behaviour from the base class (the rectangle) in the same methods (the setters).
|
|
||||||
|
|
||||||
The square class cannot be used in the same method (the boardArea method) as the rectangle class and our program keep having the same behaviour( by halving the height, the area is half for the rectangle but 1/4th for the square). That's an LSP violation.
|
|
||||||
|
|
||||||
The only way to fix this problem now, would be to create an if statement that checks in the code the type of the instance that is the board. If it would be a rectangle everything is calculated the same way, but if it is a square, after the calculation we have to multiply by the amount that we divided the height.
|
|
||||||
|
|
||||||
Whoever sees this piece of code, will have to wonder, why there is a multiplication in there and when someone wants to extend the rectangle class, by creating another child class that for example has 2:1 ratio rectangles, he better remember that he also has to go to that piece of code and add another if statement that calculates the area correctly.
|
|
||||||
|
|
||||||
## The INPC Interface example
|
|
||||||
|
|
||||||
Although an interface, doesn't contain any behaviours because the behaviours are defined in the classes that implement the interface, we can still violate the LSP. This can happen when two different classes that implement the interface, change the behaviour of how our program reacts, in their implementations.
|
|
||||||
|
|
||||||
That doesn't mean that all classes that implement a method from an interface should have the same code obviously. There is a difference of what a method does with how it does it. A violation of the LSP occurs, when the classes do different things with the same method, not when they do the same thing in a different way.
|
|
||||||
|
|
||||||
Here's an example. Suppose we have NPCs in a game and those NPCs can talk to the player character or attack him. Each NPC, when is using the `Talk` method can do different things, for example he can give a quest to the player or open the inventory to buy and sell items. The same is true for the `Attack` method: one NPC might get offended when the player says something and attack in melee, another NPC might start using ranged attacks when the player character tries to steal from him.
|
|
||||||
|
|
||||||
That's easy, we create an interface that all NPCs must implement:
|
|
||||||
|
|
||||||
```java
|
|
||||||
public interface INpc
|
|
||||||
{
|
|
||||||
void Talk(Character target);
|
|
||||||
void Attack(Character target);
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
After a while, we get to create a new NPC. A magical tree that can only give quests to the player, it can never attack him. So we decide to derive from the `INpc` interface and keep the `Attack` method empty. After all, that is the requirement, the magical tree doesn't do attacks.
|
|
||||||
|
|
||||||
Time passes and after a couple of years, we are near the completion of our game. The player has finally found the cursed book that he was looking for and he is supposed to return it to the temple. He is warned of course that he must never open the book or he is doomed.
|
|
||||||
|
|
||||||
Well, we know that there is a big chance that the player will try to open the book, so we decide that if he does this, we will freeze the player controls and all NPCs around him will start hacking till he is dead. He shouldn't have done that, so it would be time to reload from the last save.
|
|
||||||
|
|
||||||
Did you notice the bug?
|
|
||||||
|
|
||||||
If the player opens the cursed book in front of the magical tree, when there is no other NPC around, the player controls freeze and the system that is responsible for the attacks will keep calling the `INpc.Attack` method, but this method is empty for the tree. Our game will freeze. The player won't be able to move and won't die because the `Attack` method has a different behaviour from what is expected. It doesn't attack the player, it does nothing.
|
|
||||||
|
|
||||||
The solution here, is still a mess. Even if we find the bug and not our players ( which would be difficult, as we would have to remember after a couple of years that there is an NPC that his attack is not actually an attack, but it does nothing ) we would still have to create dependencies from the system that is responsible for controlling the attacks to a particular implementation, the magical tree.
|
|
||||||
|
|
||||||
Suddenly, a system that was decoupled from the rest of our program and was only dependant on an abstraction the `INpc` interface, will have if statements that check for the type of each instance of INpc and if this is of type MagicalTree do something else, for example ignore the attack. Our system now has a dependency on the MagicalTree class. Any changes to this class will have the potential to affect an unrelated system, the system that is responsible for attacking using the `INpc` interface.
|
|
||||||
|
|
||||||
By keeping, the `INpc.Attack` empty, we violated the LSP. A better way would have been to create two interfaces, for example an `INpcTalk` interface that has all the methods responsible for talking and an `INpcAttack` interface that has all the methods responsible for attacking. That way, when we were creating the MagicalTree class, we would have made it implement only the `INpcTalk` interface and the system responsible for the attacking would use only the `INpcAttack` interface. That actually is part of the next principle, the interface segregation principle, in the next post.
|
|
||||||
|
|
||||||
## Late Violation of the OCP
|
|
||||||
|
|
||||||
By looking both of the above examples, we can see that a violation of the LSP, is actually a violation of [the open closed principle](https://giannisakritidis.com/blog/The-Open-Closed-Principle/) waiting to happen.
|
|
||||||
|
|
||||||
The consequences of violating the LSP, only manifest themselves far into the future, maybe even months or years after the violation occurred. At that point, any fix will be a messy one. We would have to check code that was written long ago and create checks for specific types.
|
|
||||||
|
|
||||||
By not following the LSP, our subtypes have a different behaviour that might not affect us the moment we write them, but eventually we will have to create code that tries to eliminate that behaviour. This can only happen by creating dependencies to pieces of code, unrelated to the one we are writing now, or even worse create dependencies to implementations, in systems that up to that point were dependant only on abstractions.
|
|
||||||
|
|
||||||
## Conclusion
|
|
||||||
|
|
||||||
The LSP tells us, that the behaviour of a program should not be different if we use a subtype in place of the base type. This happens when a subtype has a different behaviour from his base type. The mechanism of creating subtypes in C# is inheritance, so a method in a child class should not do a different thing when it is called, from the one that is expected from the base class.
|
|
||||||
|
|
||||||
In the previous examples, the square setters didn't only change the relevant dimension as was happening in the rectangle class and the MagicalTree could not attack, as was expected from any other class that implemented the `INpc` interface.
|
|
||||||
|
|
||||||
This doesn't mean that child classes or classes that implement interfaces should have the same code. There is a difference on what a method does with how it does it. If we want to conform to the LSP, our methods in our subtypes should do the same thing, but in a different way.
|
|
||||||
|
|
||||||
Empty inherited methods, are usually a sign of LSP violation. Inherited methods that throw unconditional exceptions are always a LSP violation, unless the base class also throws an unconditional exception ( but why have a method in a class that only throws an exception? ).
|
|
||||||
|
|
||||||
By being careful to write code that does not violate the LSP, we can save our future self a lot of headaches and that is the point of code architecture. Investing our time now so that we save more time far into the future.
|
|
||||||
@@ -1,191 +0,0 @@
|
|||||||
---
|
|
||||||
title: "The Master Theorem For Time Complexity"
|
|
||||||
subtitle: ""
|
|
||||||
summary: "In this article, we will model the time complexity of divide and conquer using mathematical methods, analyze its asymptotic properties, and provide three methods of calculation."
|
|
||||||
coverURL: ""
|
|
||||||
time: "2023-12-18"
|
|
||||||
tags: ["algorithm", "mathematics", "computation"]
|
|
||||||
noPrompt: false
|
|
||||||
pin: false
|
|
||||||
allowShare: true
|
|
||||||
---
|
|
||||||
|
|
||||||
When we navigate through the ocean of divide and conquer, there's a question that must be addressed—how is the time complexity of divide and conquer algorithms calculated?
|
|
||||||
|
|
||||||
## From Divide and Conquer to Recurrence Relation
|
|
||||||
|
|
||||||
Divide and conquer involves breaking down a large problem into smaller subproblems and then merging the solutions of these subproblems to obtain the solution to the original problem. Recurrence relation is a mathematical way of modeling the time cost of this process.
|
|
||||||
|
|
||||||
Starting with a concrete example makes it easier to understand. Taking merge sort as an example, let $T(n)$ represent the time complexity of the original problem, where $n$ is the size of the input data. In the first split, the original data is divided into two equal parts, each of size $n/2$. Then, recursive calls to merge sort are made on these two parts, and the time complexity of this part is $2 T(n/2)$. Finally, the two sorted subarrays are merged, requiring a time complexity of $\Theta(n)$.
|
|
||||||
|
|
||||||
Based on the analysis above, we can write the recurrence relation for merge sort as follows:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{equation} T(n) = \left\{ \begin{aligned} &\Theta(1) & \text{if } n=1\\ &2 T(n/2) + \Theta(n) & \text{if } n>1 \end{aligned} \right. \tag{1} \end{equation}
|
|
||||||
$$
|
|
||||||
|
|
||||||
It can be imagined that for any divide and conquer algorithm, its time complexity can be expressed as a recurrence relation. The right-hand side of the recurrence relation usually consists of two parts: the total cost of the divided subproblems and the total cost of dividing and merging subproblems. The first part remains a function of $T$, while the second part represents the actual asymptotic complexity.
|
|
||||||
|
|
||||||
Having a recurrence relation is not sufficient to determine the exact time complexity of the algorithm. We need to further calculate the actual solution $T(n)$.
|
|
||||||
|
|
||||||
## Substitution Method
|
|
||||||
|
|
||||||
The first method for solving recurrence relations is called the substitution method. We need to guess the form of the solution first and then use mathematical induction to prove that the guess is correct.
|
|
||||||
|
|
||||||
For Equation (1), let's assume that our guess for the solution is $T(n) = O(n \log n)$. If we remove the asymptotic notation, this equation is equivalent to $T(n) \le c_1 n \log n$, where $c_1$ is any positive constant.
|
|
||||||
|
|
||||||
According to mathematical induction, we first need to establish that the guess holds for small values of $n$. When $n=1$, according to Equation (1), $T(1) = \Theta(1) = d_1$, where $d_1$ is some constant greater than 0. According to the guess, we hope $T(1) \le c_1 \log 1 = 0$, but no matter how we choose $c_1$, this equation cannot hold because $T(1) = d_1$ is always greater than 0. The mathematical induction fails before it even starts.
|
|
||||||
|
|
||||||
However, there is no need to worry; this is just a special case caused by $ \log 1 = 0$. We can place the initial state of mathematical induction at $n>1$ without affecting the results of mathematical induction. We are only interested in the asymptotic properties of $T(n)$ when $n$ is sufficiently large, not in the initial stage.
|
|
||||||
|
|
||||||
Now, let $n = 2$, then $T(2) = 2T(1) + d_2 = 2d_1 + d_2$. We hope that $T(2) \le c_1 \log 2$ holds. Simplifying, we get $c_1 \ge d_1 + d_2/2$. Since $d_1$ and $d_2$ are constants, such $c_1$ exists, and the initial condition holds.
|
|
||||||
|
|
||||||
Next, mathematical induction assumes that the solution holds at $n/2$, i.e., $T(n/2) \le c_1 \frac{n}{2} \log\frac{n}{2} = \frac{1}{2}c_1n(\log n - 1)$. Then we prove that $T(n) \le c_1 n \log n$ also holds.
|
|
||||||
|
|
||||||
Substituting $T(n/2)$ into Equation (1), we get
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{equation} \begin{aligned} T(n) & = 2 T\left(\frac{n}{2}\right) + \Theta(n) \\ & \le 2 \frac{1}{2}c_1n(\log n - 1) + d_2n \\ & = c_1 n \log n + (d_2 - c_1) n \\ & \le c_1 n \log n \end{aligned} \end{equation}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Where the last line's inequality requires $d_2 - c_1 < 0$, obviously such $c_1$ exists, so the proof is complete.
|
|
||||||
|
|
||||||
Thus, we have proved that $T(n) = O(n \log n)$ is the solution to the recurrence relation (1). However, this is not the end; this asymptotic notation is not a tight bound. Can we further guess that $T(n) = \Theta(n \log n)$ holds? This is indeed a good idea. So, as we proceed, as long as we can prove that $T(n) = \Omega(n \log n)$ holds, we can obtain the tight bound mentioned above. Removing the asymptotic notation, this equation is equivalent to $T(n) \ge c_2 n \log n$. Using mathematical induction again, confirming that this holds in the initial stage, and then assuming that the solution holds at $n/2$, we can derive that the solution holds at $n$. Therefore, the proof is complete. Since the proof steps are almost identical to those just mentioned, we will not elaborate on them, and you can try it yourself.
|
|
||||||
|
|
||||||
The substitution method relies on accurate guesses, which can be impractical. Therefore, in practice, a more common approach is to find a guess using other methods and then use the substitution method to verify the guess. The recursive tree method we will introduce next provides this possibility.
|
|
||||||
|
|
||||||
## Recursive Tree
|
|
||||||
|
|
||||||
Expanding the recurrence relation layer by layer directly yields a tree structure. For example, let's take $T(n) = 3 T(n/4) + \Theta(n^2)$ as an example and see how to draw its recursive tree.
|
|
||||||
|
|
||||||
Expanding the first layer, we draw three child nodes under the root node.
|
|
||||||
|
|
||||||
Here, $cn^2$ represents the cost of decomposition and merging at this layer, which corresponds to the part represented by $\Theta(n^2)$ in the recurrence relation.
|
|
||||||
|
|
||||||
Next, further expand to the second layer.
|
|
||||||
|
|
||||||
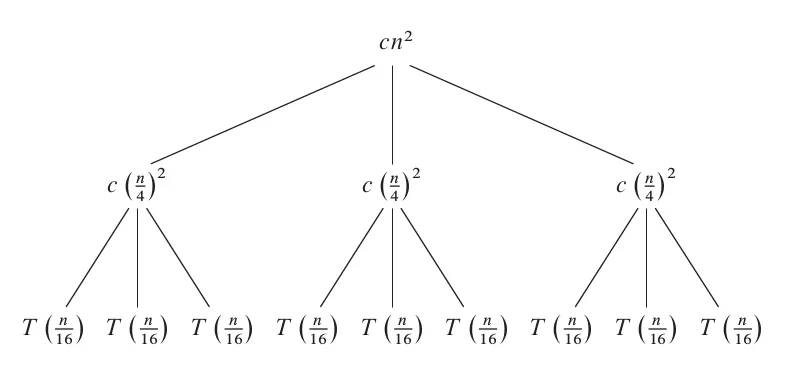
|
|
||||||
|
|
||||||
Here, the cost of each node in the first layer is still $c(\frac{n}{4})^2$, still corresponding to the part represented by $\Theta(n^2)$ in the recurrence relation, but the data size has changed from $n$ to $n/4$.
|
|
||||||
|
|
||||||
Continue expanding in this way until the leaf nodes.
|
|
||||||
|
|
||||||
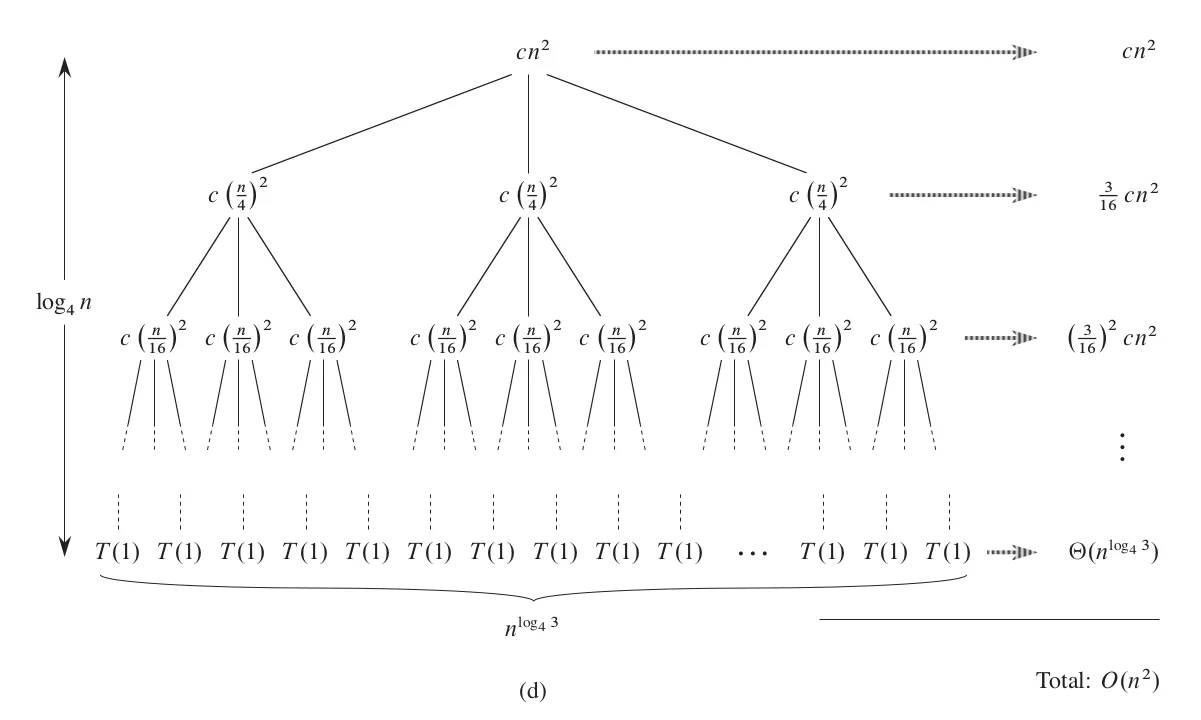
|
|
||||||
|
|
||||||
This completes a complete recursive tree. The data size of each layer is reduced to one-fourth of the previous one, until the data size of the leaf node is 1, so the total number of layers is $\log_4 n$. The rightmost side of the figure calculates the total cost of all nodes in each layer, and the calculation is simple: multiply the cost of a single node by the number of nodes in that layer. In the last layer, the cost of a single node is a constant, and the number of nodes is $3^{\log_4 n} = n^{\log_4 3}$, and we denote the total cost as $\Theta(n^{\log_4 3})$.
|
|
||||||
|
|
||||||
Next, we just need to add up the costs of all nodes to obtain the solution to the recurrence relation.
|
|
||||||
|
|
||||||
$$
|
|
||||||
\begin{aligned} T(n) &= cn^2 + \frac{3}{16} cn^2 + \left(\frac{3}{16}\right)^2 cn^2 + \cdots + \left( \frac{3}{16} \right)^{\log_4 n-1} cn^2 + \Theta(n^{\log_4 3}) \\ &=\sum_{i=0}^{\log_4 n-1}{\left(\frac{3}{16}\right)^i cn^2} + \Theta(n^{\log_4 3})\\ &\lt \sum_{i=0}^{\infty}{\left(\frac{3}{16}\right)^i cn^2} + \Theta(n^{\log_4 3}) \\ &= \frac{1}{1 - 3/16}cn^2 + \Theta(n^{\log_4 3}) \\ &= \frac{16}{13} cn^2 + \Theta(n^{\log_4 3}) \\ &= O(n^2) \end{aligned}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Here, in the third line, we made a simplification by replacing a finite geometric series with an infinite geometric series. Although the total size has increased, this infinite decreasing geometric series has a limit, so this replacement can simplify the derivation process. The second term in the fifth line is a lower-order term relative to the first term, so it is discarded, resulting in the final result.
|
|
||||||
|
|
||||||
Similar to before, we have only proven the upper bound of the recurrence relation. Naturally, we want to try whether it can also be proven as a lower bound. In the above equation, each term in the summation contains $cn^2$, and each term is positive, so $T(n) = \Omega(n^2)$ obviously holds. Therefore, the solution to the recurrence relation is $T(n) = \Theta(n^2)$.
|
|
||||||
|
|
||||||
In this example, we directly calculated the solution to the recurrence relation using the recursive tree method. Of course, we can use the substitution method to verify whether this solution is correct. In some cases, it may be slightly difficult to calculate the exact solution using the recursive tree method, but it does not prevent us from making a reasonable guess and then further verifying this guess using the substitution method.
|
|
||||||
|
|
||||||
## Master Theorem
|
|
||||||
|
|
||||||
Both the substitution method and the recursion tree method have their drawbacks. The former requires an accurate guess, while the latter involves drawing a recursion tree and deriving results. If you derive too much, you may find that the forms of most recursive solutions seem to be the same. From the derivation process above, it can be observed that the final solution depends entirely on the sum of costs in the middle layers and has nothing to do with the leaf layer because the latter is a lower-order term. In other recursion trees, the final solution may depend entirely on the cost of the leaf layer, unrelated to the middle layers. Therefore, we may be able to classify recursive formulas and directly write out the final solution according to some rules. This is the idea behind the master theorem.
|
|
||||||
|
|
||||||
When the divide-and-conquer method evenly splits the data each time, the recursive formula generally has the following form.
|
|
||||||
|
|
||||||
$$
|
|
||||||
T(n) = aT\left(\frac{n}{b}\right) + f(n) \tag{2}
|
|
||||||
$$
|
|
||||||
|
|
||||||
where $a$ is a positive integer representing the number of subproblems when dividing each time, $b$ is an integer greater than 1 representing the reduction factor in problem size each time, and $f(n)$ is an asymptotically positive function representing the cost of dividing and merging.
|
|
||||||
|
|
||||||
To find a unified solution applicable to any $a$, $b$, and $f(n)$, we still need to use the recursion tree to calculate the costs of all intermediate and leaf nodes and try to derive a simple result.
|
|
||||||
|
|
||||||
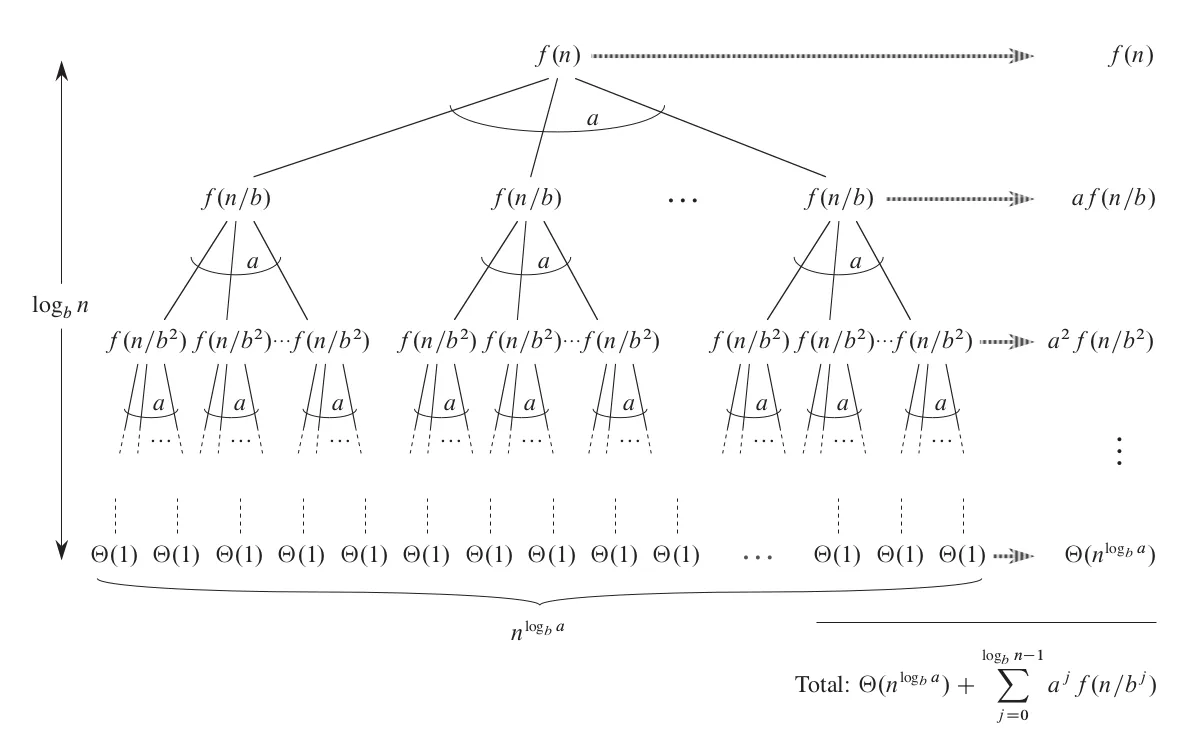
|
|
||||||
|
|
||||||
From the graph, we can see that the total cost of all nodes is $T(n) = \Theta(n^{\log_b a}) + \sum_{j=0}^{\log_b n-1}{a^j f(n/b^j)}$. Further derivation requires a breakthrough idea, and I don't know how the original researchers discovered the following pattern, but it is indeed magical.
|
|
||||||
|
|
||||||
Researchers found that the relationship between $f(n)$ and $\Theta(n^{\log_b a})$ determines the final simplified form of $\sum_{j=0}^{\log_b n-1}{a^j f(n/b^j)}$. Define
|
|
||||||
|
|
||||||
$$
|
|
||||||
g(n) = \sum_{j=0}^{\log_b n-1}{a^j f(n/b^j)} \tag{3}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Now let's analyze three cases.
|
|
||||||
|
|
||||||
1. If $\Theta(n^{\log_b a})$ is larger, we can assume that there exists a constant $\epsilon > 0$ such that $f(n) = O(n^{\log_b a-\epsilon})$. Substituting this into the summation formula, it can be simplified to $g(n) = O(n^{\log_b a})$.
|
|
||||||
|
|
||||||
2. If both are equally large, directly substitute into equation (3) and simplify to get $g(n) = \Theta(n^{\log_b a} \log n)$.
|
|
||||||
|
|
||||||
3. If $f(n)$ is larger and, for some constant $c < 1$, for all sufficiently large $n$, $a f(n/b) \le c f(n)$ holds, then it can be deduced that $g(n) = \Theta(f(n))$.
|
|
||||||
|
|
||||||
Here, the complete proof process is not provided, partly because I don't want to make it too long, and secondly, I feel that these proofs are somewhat cumbersome and not very meaningful. Interested students can refer to the original book.
|
|
||||||
|
|
||||||
Substituting the functions $g(n)$ for these three cases into the complete solution, we get:
|
|
||||||
|
|
||||||
- For case 1: $T(n) = \Theta(n^{\log_b a}) + O(n^{\log_b a}) = \Theta(n^{\log_b a})$
|
|
||||||
|
|
||||||
- For case 2: $T(n) = \Theta(n^{\log_b a}) + \Theta(n^{\log_b a} \log n) = \Theta(n^{\log_b a} \log n)$
|
|
||||||
|
|
||||||
- For case 3: $T(n) = \Theta(n^{\log_b a}) + \Theta(f(n)) = \Theta(f(n))$
|
|
||||||
|
|
||||||
Now, for any recursive formula, we only need to determine which case it belongs to and directly substitute into the corresponding formula. To facilitate understanding, let's go through a few examples.
|
|
||||||
|
|
||||||
**Example 1:**
|
|
||||||
|
|
||||||
$T(n) = 9 T(n/3) + n$
|
|
||||||
|
|
||||||
For this recursive formula, we have $a = 9$, $b = 3$, $f(n) = n$. Since $f(n) = n$ is asymptotically smaller than $\Theta(n^2)$, it can be applied to the first case of the master theorem, and the solution is $T(n) = \Theta(n^2)$.
|
|
||||||
|
|
||||||
**Example 2:**
|
|
||||||
|
|
||||||
$T(n) = T(2n/3) + 1$
|
|
||||||
|
|
||||||
For this formula, $a = 1$, $b = 3/2$, $f(n) = 1$. Since $n^{\log_b a} = n^{\log_{3/2} 1} = n^0 = 1$, which is exactly equal to $f(n)$, it can be applied to the second case of the master theorem, and the solution is $T(n) = \Theta(\log n)$.
|
|
||||||
|
|
||||||
**Example 3:**
|
|
||||||
|
|
||||||
$T(n) = 3T(n/4) + n\log n$
|
|
||||||
|
|
||||||
For this formula, $a = 3$, $b = 4$, $f(n) = n\log n$. Since $n^{\log_b a} = n^{\log_4 3} = n^{0.793}$, and $f(n) = n\log n$ is asymptotically larger than $n^{0.793}$, it should consider the third case of the master theorem. However, we need to check if the additional condition holds: for some constant $c < 1$ and all sufficiently large $n$, $a f(n/b) \le c f(n)$ holds. Substituting $a$, $b$, and $f(n)$ into the inequality, we get
|
|
||||||
|
|
||||||
$$
|
|
||||||
3\frac{n}{4}\log\frac{n}{4} \le cn\log n \implies \frac{3}{4}( \log n - 2) \le c\log n \implies \left(\frac{3}{4} - c\right) \log n \le \frac{3}{2}
|
|
||||||
$$
|
|
||||||
|
|
||||||
When $c \ge \frac{3}{4}$, this inequality always holds, and the additional condition is satisfied. Therefore, it can be applied to the third case of the master theorem, and the solution is $T(n) = \Theta(n\log n)$.
|
|
||||||
|
|
||||||
**Example 4:**
|
|
||||||
|
|
||||||
$T(n) = 2T(n/2) + n\log n$
|
|
||||||
|
|
||||||
For this formula, $a = 2$, $b = 2$, $f(n) = n\log n$. Since $n^{\log_b a} = n^{\log_2 2} = n$, and $f(n) = n\log n$ is asymptotically larger than $n$, it should consider the third case of the master theorem. Substituting $a$, $b$, and $f(n)$ into the inequality, we get
|
|
||||||
|
|
||||||
$$
|
|
||||||
2\frac{n}{2}\log\frac{n}{2} \le cn\log n \implies \log n - 1 \le c\log n \implies (1-c)\log n \le 1
|
|
||||||
$$
|
|
||||||
|
|
||||||
When $c \ge 1$, this inequality always holds. However, the additional condition requires $c < 1$, so this case cannot be applied to the third case of the master theorem. In other words, not all recursive formulas of the form $T(n) = a T(n/b) + f(n)$ can be solved using the master theorem; there is a gap between cases two and three. In such cases, we can only use the recursion tree method. Students can try it, and the result will be $T(n) = \Theta(n \log^2 n)$.
|
|
||||||
|
|
||||||
After going through these four examples, have you mastered the master theorem? If you have any questions, please leave a comment, and I will reply as soon as possible.
|
|
||||||
|
|
||||||
The study of algorithms is endless, and the calculation of time complexity is fundamental and should not be underestimated.
|
|
||||||
|
|
||||||
## Details
|
|
||||||
|
|
||||||
Careful readers may notice that in the fourth case mentioned above, although $nlgn$ grows asymptotically faster than $n$, it is not asymptotically greater in the polynomial sense because there is no $\epsilon > 0$ such that $nlgn = \Omega \left( n^{1+\epsilon} \right)$ holds. On the contrary, $nlgn = o \left( n^{1+\epsilon} \right)$ holds for any $\epsilon > 0$. So, in fact, this case does not need to be judged for regular conditions to draw conclusions in advance. However, in the third case in the previous text, I did not emphasize asymptotic greater in the polynomial sense, not because I forgot to write it, but because this condition is not needed at all.
|
|
||||||
|
|
||||||
For any recurrence relation that fits the master theorem format, if it satisfies the regular conditions in case three, then it must satisfy $f\left(n\right) = \Omega \left( n^{log_b a + \epsilon} \right)$." The specific proof details can be found in [this answer](https://cs.stackexchange.com/a/121749/128497) on StackExchange, and are not detailed here.
|
|
||||||
|
|
||||||
Although regular conditions can imply $f\left(n\right) = \Omega \left( n^{log_b a + \epsilon} \right)$, the reverse is not true. We can construct the following function:
|
|
||||||
|
|
||||||
$T\left(n\right) = T\left(n/2\right) + n\left( 2 - \cos n \right)$
|
|
||||||
|
|
||||||
Here, $a=1$, $b=2$, and $f\left(n\right) = n \left( 2 - \cos n \right) = \Omega \left( n^{log_2 1+ \epsilon} \right) = \Omega \left( n^\epsilon \right)$ holds for any $\epsilon \le1$. However, when applying the regular condition:
|
|
||||||
|
|
||||||
$\begin{aligned} f\left(n / 2\right) &\le c f\left(n\right) \\ \frac{n}{2} \left(2 - \cos \frac{n}{2} \right) & \le c \left( 2 - \cos n \right) \end{aligned}$
|
|
||||||
|
|
||||||
For any $c \lt 1$, the right side must be $c \left( 2 - \cos n \right) \lt 3$. However, the left side, when $n$ is large enough, must be greater than $3$. Therefore, this equation cannot hold, and the regular condition is not satisfied.
|
|
||||||
|
|
||||||
## Reference
|
|
||||||
|
|
||||||
These cases are from the Wikipedia entry on [Master theorem](<https://en.wikipedia.org/w/index.php?title=Master_theorem_(analysis_of_algorithms)§ion=7#Inadmissible_equations>).
|
|
||||||
@@ -1,139 +0,0 @@
|
|||||||
---
|
|
||||||
title: "everything you ever wanted to know about the computer vision"
|
|
||||||
summary: "One of the most powerful and compelling types of AI is computer vision which you’ve almost surely experienced in any number of ways without even knowing. Here’s a look at what it is, how it works, and why it’s so awesome (and is only going to get better)."
|
|
||||||
coverURL: "https://miro.medium.com/v2/resize:fit:788/1*8gmgaAkFdI-9OHY5cA93xQ.png"
|
|
||||||
time: "2023-12-25"
|
|
||||||
tags: ["computer-vision"]
|
|
||||||
noPrompt: false
|
|
||||||
pin: false
|
|
||||||
allowShare: true
|
|
||||||
---
|
|
||||||
|
|
||||||
> This post is used to preview the display effect of long articles. The author is Ilija Mihajlovic and is reproduced in [here](https://towardsdatascience.com/everything-you-ever-wanted-to-know-about-computer-vision-heres-a-look-why-it-s-so-awesome-e8a58dfb641e)
|
|
||||||
|
|
||||||
One of the most powerful and compelling types of AI is computer vision which you’ve almost surely experienced in any number of ways without even knowing. Here’s a look at what it is, how it works, and why it’s so awesome (and is only going to get better).
|
|
||||||
|
|
||||||
Computer vision is the field of computer science that focuses on replicating parts of the complexity of the human vision system and enabling computers to identify and process objects in images and videos in the same way that humans do. Until recently, computer vision only worked in limited capacity.
|
|
||||||
|
|
||||||
Thanks to advances in artificial intelligence and innovations in deep learning and neural networks, the field has been able to take great leaps in recent years and has been able to surpass humans in some tasks related to detecting and labeling objects.
|
|
||||||
|
|
||||||
One of the driving factors behind the growth of computer vision is the amount of data we generate today that is then used to train and make computer vision better.
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
Along with a tremendous amount of visual data (_more than 3 billion images are shared online every day_), the computing power required to analyze the data is now accessible. As the field of computer vision has grown with new hardware and algorithms so has the accuracy rates for object identification. In less than a decade, today’s systems have reached 99 percent accuracy from 50 percent making them more accurate than humans at quickly reacting to visual inputs.
|
|
||||||
|
|
||||||
Early experiments in computer vision started in the 1950s and it was first put to use commercially to distinguish between typed and handwritten text by the 1970s, today the applications for computer vision have grown exponentially.
|
|
||||||
|
|
||||||
> By 2022, the computer vision and hardware market is expected to reach $48.6 billion
|
|
||||||
|
|
||||||
## How Does Computer Vision Work?
|
|
||||||
|
|
||||||
One of the major open questions in both Neuroscience and Machine Learning is: How exactly do our brains work, and how can we approximate that with our own algorithms? The reality is that there are very few working and comprehensive theories of brain computation; so despite the fact that Neural Nets are supposed to “mimic the way the brain works,” nobody is quite sure if that’s actually true.
|
|
||||||
|
|
||||||
The same paradox holds true for computer vision — since we’re not decided on how the brain and eyes process images, it’s difficult to say how well the algorithms used in production approximate our own internal mental processes.
|
|
||||||
|
|
||||||
On a certain level Computer vision is all about pattern recognition. So one way to train a computer how to understand visual data is to feed it images, lots of images thousands, millions if possible that have been labeled, and then subject those to various software techniques, or algorithms, that allow the computer to hunt down patterns in all the elements that relate to those labels.
|
|
||||||
|
|
||||||
So, for example, if you feed a computer a million images of cats (we all love them😄😹), it will subject them all to algorithms that let them analyze the colors in the photo, the shapes, the distances between the shapes, where objects border each other, and so on, so that it identifies a profile of what “cat” means. When it’s finished, the computer will (in theory) be able to use its experience if fed other unlabeled images to find the ones that are of cat.
|
|
||||||
|
|
||||||
Let’s leave our fluffy cat ==friends== for a moment on the side and let’s get more technical🤔😹. Below is a simple illustration of the grayscale image buffer which stores our image of Abraham Lincoln. Each pixel’s brightness is represented by a single 8-bit number, whose range is from 0 (black) to 255 (white):
|
|
||||||
|
|
||||||
 on Unsplash](https://miro.medium.com/v2/resize:fit:788/0*CI5wgSszZnpHu5Ip.png)
|
|
||||||
|
|
||||||
```plaintext
|
|
||||||
{ 157, 153, 174, 168, 150, 152, 129, 151, 172, 161, 155, 156, 155, 182, 163, 74, 75, 62, 33, 17, 110, 210, 180, 154, 180, 180, 50, 14, 34, 6, 10, 33, 48, 106, 159, 181, 206, 109, 5, 124, 131, 111, 120, 204, 166, 15, 56, 180,194, 68, 137, 251, 237, 239, 239, 228, 227, 87, 71, 201, 172, 105, 207, 233, 233, 214, 220, 239, 228, 98, 74, 206, 188, 88, 179, 209, 185, 215, 211, 158, 139, 75, 20, 169, 189, 97, 165, 84, 10, 168, 134, 11, 31, 62, 22, 148, 199, 168, 191, 193, 158, 227, 178, 143, 182, 106, 36, 190, 205, 174, 155, 252, 236, 231, 149, 178, 228, 43, 95, 234, 190, 216, 116, 149, 236, 187, 86, 150, 79, 38, 218, 241, 190, 224, 147, 108, 227, 210, 127, 102, 36, 101, 255, 224, 190, 214, 173, 66, 103, 143, 96, 50, 2, 109, 249, 215, 187, 196, 235, 75, 1, 81, 47, 0, 6, 217, 255, 211, 183, 202, 237, 145, 0, 0, 12, 108, 200, 138, 243, 236, 195, 206, 123, 207, 177, 121, 123, 200, 175, 13, 96, 218 };
|
|
||||||
```
|
|
||||||
|
|
||||||
This way of storing image data may run counter to your expectations, since the data certainly *appears* to be two-dimensional when it is displayed. Yet, this is the case, since computer memory consists simply of an ever-increasing linear list of address spaces.
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
Let’s go back to the first picture again and imagine adding a colored one. Now things start to get more complicated. Computers usually read color as a series of 3 values — red, green, and blue (RGB) — on that same 0–255 scale. Now, each pixel actually has 3 values for the computer to store in addition to its position. If we were to colorize President Lincoln, that would lead to 12 x 16 x 3 values, or 576 numbers.
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
That’s a lot of memory to require for one image, and a lot of pixels for an algorithm to iterate over. But to train a model with meaningful accuracy especially when you’re talking about Deep Learning you’d usually need tens of thousands of images, and the more the merrier.
|
|
||||||
|
|
||||||
## The Evolution Of Computer Vision
|
|
||||||
|
|
||||||
Before the advent of deep learning, the tasks that computer vision could perform were very limited and required a lot of manual coding and effort by developers and human operators. For instance, if you wanted to perform facial recognition, you would have to perform the following steps:
|
|
||||||
|
|
||||||
- **Create a database**: You had to capture individual images of all the subjects you wanted to track in a specific format.
|
|
||||||
- **Annotate images**: Then for every individual image, you would have to enter several key data points, such as distance between the eyes, the width of nose bridge, distance between upper-lip and nose, and dozens of other measurements that define the unique characteristics of each person.
|
|
||||||
- **Capture new images**: Next, you would have to capture new images, whether from photographs or video content. And then you had to go through the measurement process again, marking the key points on the image. You also had to factor in the angle the image was taken.
|
|
||||||
|
|
||||||
After all this manual work, the application would finally be able to compare the measurements in the new image with the ones stored in its database and tell you whether it corresponded with any of the profiles it was tracking. In fact, there was very little automation involved and most of the work was being done manually. And the error margin was still large.
|
|
||||||
|
|
||||||
Machine learning provided a different approach to solving computer vision problems. With machine learning, developers no longer needed to manually code every single rule into their vision applications. Instead they programmed “features,” smaller applications that could detect specific patterns in images. They then used a statistical learning algorithm such as linear regression, logistic regression, decision trees or support vector machines (SVM) to detect patterns and classify images and detect objects in them.
|
|
||||||
|
|
||||||
Machine learning helped solve many problems that were historically challenging for classical software development tools and approaches. For instance, years ago, machine learning engineers were able to create a software that could predict breast cancer survival windows better than human experts. However building the features of the software required the efforts of dozens of engineers and breast cancer experts and took a lot of time develop.
|
|
||||||
|
|
||||||
Deep learning provided a fundamentally different approach to doing machine learning. Deep learning relies on neural networks, a general-purpose function that can solve any problem representable through examples. When you provide a neural network with many labeled examples of a specific kind of data, it’ll be able to extract common patterns between those examples and transform it into a mathematical equation that will help classify future pieces of information.
|
|
||||||
|
|
||||||
For instance, creating a facial recognition application with deep learning only requires you to develop or choose a preconstructed algorithm and train it with examples of the faces of the people it must detect. Given enough examples (lots of examples), the neural network will be able to detect faces without further instructions on features or measurements.
|
|
||||||
|
|
||||||
Deep learning is a very effective method to do computer vision. In most cases, creating a good deep learning algorithm comes down to gathering a large amount of labeled training data and tuning the parameters such as the type and number of layers of neural networks and training epochs. Compared to previous types of machine learning, deep learning is both easier and faster to develop and deploy.
|
|
||||||
|
|
||||||
Most of current computer vision applications such as cancer detection, self-driving cars and facial recognition make use of deep learning. Deep learning and deep neural networks have moved from the conceptual realm into practical applications thanks to availability and advances in hardware and cloud computing resources.
|
|
||||||
|
|
||||||
## How Long Does It Take To Decipher An Image
|
|
||||||
|
|
||||||
In short not much. That’s the key to why computer vision is so thrilling: Whereas in the past even supercomputers might take days or weeks or even months to chug through all the calculations required, today’s ultra-fast chips and related hardware, along with the a speedy, reliable internet and cloud networks, make the process lightning fast. Once crucial factor has been the willingness of many of the big companies doing AI research to share their work Facebook, Google, IBM, and Microsoft, notably by open sourcing some of their machine learning work.
|
|
||||||
|
|
||||||
This allows others to build on their work rather than starting from scratch. As a result, the AI industry is cooking along, and experiments that not long ago took weeks to run might take 15 minutes today. And for many real-world applications of computer vision, this process all happens continuously in microseconds, so that a computer today is able to be what scientists call “situationally aware.”
|
|
||||||
|
|
||||||
## Applications Of Computer Vision
|
|
||||||
|
|
||||||
Computer vision is one of the areas in Machine Learning where core concepts are already being integrated into major products that we use every day.
|
|
||||||
|
|
||||||
## CV In Self-Driving Cars
|
|
||||||
|
|
||||||
But it’s not just tech companies that are leverage Machine Learning for image applications.
|
|
||||||
|
|
||||||
Computer vision enables self-driving cars to make sense of their surroundings. Cameras capture video from different angles around the car and feed it to computer vision software, which then processes the images in real-time to find the extremities of roads, read traffic signs, detect other cars, objects and pedestrians. The self-driving car can then steer its way on streets and highways, avoid hitting obstacles, and (hopefully) safely drive its passengers to their destination.
|
|
||||||
|
|
||||||
## CV In Facial Recognition
|
|
||||||
|
|
||||||
Computer vision also plays an important role in facial recognition applications, the technology that enables computers to match images of people’s faces to their identities. Computer vision algorithms detect facial features in images and compare them with databases of face profiles. Consumer devices use facial recognition to authenticate the identities of their owners. Social media apps use facial recognition to detect and tag users. Law enforcement agencies also rely on facial recognition technology to identify criminals in video feeds.
|
|
||||||
|
|
||||||
## CV In Augmented Reality & Mixed Reality
|
|
||||||
|
|
||||||
Computer vision also plays an important role in augmented and mixed reality, the technology that enables computing devices such as smartphones, tablets and smart glasses to overlay and embed virtual objects on real world imagery. Using computer vision, AR gear detect objects in real world in order to determine the locations on a device’s display to place a virtual object. For instance, computer vision algorithms can help AR applications detect planes such as tabletops, walls and floors, a very important part of establishing depth and dimensions and placing virtual objects in physical world.
|
|
||||||
|
|
||||||
## CV In Healthcare
|
|
||||||
|
|
||||||
Computer vision has also been an important part of advances in health-tech. Computer vision algorithms can help automate tasks such as detecting cancerous moles in skin images or finding symptoms in x-ray and MRI scans.
|
|
||||||
|
|
||||||
## Challenges of Computer Vision
|
|
||||||
|
|
||||||
Helping computers to see turns out to be very hard.
|
|
||||||
|
|
||||||
Inventing a machine that sees like we do is a deceptively difficult task, not just because it’s hard to make computers do it, but because we’re not entirely sure how human vision works in the first place.
|
|
||||||
|
|
||||||
Studying biological vision requires an understanding of the perception organs like the eyes, as well as the interpretation of the perception within the brain. Much progress has been made, both in charting the process and in terms of discovering the tricks and shortcuts used by the system, although like any study that involves the brain, there is a long way to go.
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
Many popular computer vision applications involve trying to recognize things in photographs; for example:
|
|
||||||
|
|
||||||
- **Object Classification**: What broad category of object is in this photograph?
|
|
||||||
- **Object Identification**: Which type of a given object is in this photograph?
|
|
||||||
- **Object Verification**: Is the object in the photograph?
|
|
||||||
- **Object Detection**: Where are the objects in the photograph?
|
|
||||||
- **Object Landmark Detection**: What are the key points for the object in the photograph?
|
|
||||||
- **Object Segmentation**: What pixels belong to the object in the image?
|
|
||||||
- **Object Recognition**: What objects are in this photograph and where are they?
|
|
||||||
|
|
||||||
Outside of just recognition, other methods of analysis include:
|
|
||||||
|
|
||||||
- **Video motion analysis** uses computer vision to estimate the velocity of objects in a video, or the camera itself.
|
|
||||||
- In **image segmentation**, algorithms partition images into multiple sets of views.
|
|
||||||
- **Scene reconstruction** creates a 3D model of a scene inputted through images or video.
|
|
||||||
- In **image restoration**, noise such as blurring is removed from photos using Machine Learning based filters.
|
|
||||||
|
|
||||||
Any other application that involves understanding pixels through software can safely be labeled as computer vision.
|
|
||||||
|
|
||||||
## Conclusion
|
|
||||||
|
|
||||||
Despite the recent progress, which has been impressive, we’re still not even close to solving computer vision. However, there are already multiple healthcare institutions and enterprises that have found ways to apply CV systems, powered by CNNs, to real-world problems. And this trend is not likely to stop anytime soon.
|
|
||||||
@@ -1,704 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Taylor formula, taylor theorem, taylor series, taylor expansion"
|
|
||||||
subtitle: ""
|
|
||||||
summary: "This article mainly introduces the content and connection between the four concepts of Taylor's formula, Taylor's theorem, Taylor series and Taylor's expansion."
|
|
||||||
coverURL: ""
|
|
||||||
time: "2024-03-06"
|
|
||||||
tags: ["mathematics"]
|
|
||||||
noPrompt: false
|
|
||||||
pin: false
|
|
||||||
allowShare: true
|
|
||||||
---
|
|
||||||
|
|
||||||
## Taylor Formula
|
|
||||||
|
|
||||||
If the function $f(x)$ is differentiable at point $x_{0}$, i.e.,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{x \rightarrow x_{0}}{\frac{f(x)-f(x_{0})}{x-x_{0}}}=f'(x_{0})
|
|
||||||
$$
|
|
||||||
|
|
||||||
which is also expressed as
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{x \rightarrow x_{0}}{\frac{f(x)-f(x_{0})}{x-x_{0}}}-f'(x_{0})=0
|
|
||||||
$$
|
|
||||||
|
|
||||||
Rearranging gives
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{x \rightarrow x_{0}}{\frac{f(x)-f(x_{0})-f'(x_{0})(x-x_{0})}{x-x_{0}}}=0
|
|
||||||
$$
|
|
||||||
|
|
||||||
Thus,
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)-f(x_{0})-f'(x_{0})(x-x_{0})=o(x-x_{0})(x\rightarrow x_{0})
|
|
||||||
$$
|
|
||||||
|
|
||||||
Rearranging terms yields
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})(x\rightarrow x_{0})
|
|
||||||
$$
|
|
||||||
|
|
||||||
This implies that near the point $x*{0}$, we can approximate the function $f(x)$ with a first-degree polynomial $f(x*{0})+f'(x*{0})(x-x*{0})$, with an error of $(x-x*{0})$ as a higher-order infinitesimal. Sometimes, such an approximation may be crude, indicating a relatively large error. Thus, naturally, we wonder if we can approximate $f(x)$ using a higher-degree $n$ polynomial to make the error $o((x-x*{0})^{n})$.
|
|
||||||
|
|
||||||
For a polynomial function
|
|
||||||
|
|
||||||
$$
|
|
||||||
f_{n}(x)=a_{0}+a_{1}(x-x_{0})+a_{2}((x-x_{0})^{2})+...+a_{n}((x-x_{0})^{n})
|
|
||||||
$$
|
|
||||||
|
|
||||||
By successively taking its derivatives at $x_{0}$, we obtain
|
|
||||||
|
|
||||||
$$
|
|
||||||
f_{n}(x_{0})=a_{0} \\
|
|
||||||
f_{n}'(x_{0})=a_{1} \\
|
|
||||||
f_{n}''(x_{0})=2!a_{2} \\
|
|
||||||
... \\
|
|
||||||
f_{n}^{(n)}(x_{0})=n!a_{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Therefore,
|
|
||||||
|
|
||||||
$$
|
|
||||||
a_{0}=f_{n}(x_{0}) \\
|
|
||||||
a_{1}=\frac{f_{n}'(x_{0})}{1!} \\
|
|
||||||
a_{2}=\frac{f_{n}''(x_{0})}{2!} \\
|
|
||||||
a_{n}=\frac{f_{n}^{(n)}(x_{0})}{n!}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Thus, the coefficients of the polynomial function $f*{n}(x)$ are uniquely determined by its derivatives at point $x*{0}$. This insight inspires us that for a general function $f(x)$, if $f(x)$ has derivatives up to $n$th order at point $x_{0}$, then these derivatives uniquely determine an $n$th degree polynomial
|
|
||||||
|
|
||||||
$$
|
|
||||||
T_{n}(x)=f(x_{0})+\frac{f'(x_{0})}{1!}(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2} \\ +...+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
This polynomial is called the **Taylor polynomial** of function $f(x)$ at point $x*{0}$, and the coefficients of $T*{n}(x)$
|
|
||||||
|
|
||||||
$$
|
|
||||||
\frac{f^{(k)}(x_{0})}{k!}(k=1,2,...,n)
|
|
||||||
$$
|
|
||||||
|
|
||||||
are termed as **Taylor coefficients**.
|
|
||||||
|
|
||||||
It is evident that the function $f(x)$ and its Taylor polynomial $T*{n}(x)$ have the same function values and derivatives up to the $n$th order at point $x*{0}$, i.e.,
|
|
||||||
|
|
||||||
$$
|
|
||||||
f^{(k)}(x_{0})=T_{n}^{(k)}(x_{0}),\ k=0,1,2,...,n.
|
|
||||||
$$
|
|
||||||
|
|
||||||
Returning to our conjecture, can we prove $f(x)=T*{n}(x)+o((x-x*{0})^{n})$? If this holds, then when approximating function $f(x)$ with the Taylor polynomial $T*{n}(x)$, the error will be as desired, i.e., an error term higher order than $(x-x*{0})^{n}$.
|
|
||||||
|
|
||||||
**Theorem:** If the function $f(x)$ has derivatives up to $n$th order at point $x_{0}$, then
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=T_{n}(x)+ o((x-x_{0})^{n})
|
|
||||||
$$
|
|
||||||
|
|
||||||
i.e.,
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=f(x_{0})+\frac{f'(x_{0})}{1!}(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2} +\\...+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+o((x-x_{0})^{n})
|
|
||||||
$$
|
|
||||||
|
|
||||||
**Proof:** Let
|
|
||||||
|
|
||||||
$$
|
|
||||||
R_{n}(x)=f(x)-T_{n}(x)\\
|
|
||||||
Q_{n}(x)=(x-x_{0})^{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
It is to be proven that
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{x \rightarrow x_{0}}{\frac{R_{n}(x)}{Q_{n}(x)}}=0
|
|
||||||
$$
|
|
||||||
|
|
||||||
Since
|
|
||||||
|
|
||||||
$$
|
|
||||||
f^{(k)}(x_{0})=T_{n}^{(k)}(x_{0}),\ k=0,1,2,...,n.
|
|
||||||
$$
|
|
||||||
|
|
||||||
Thus,
|
|
||||||
|
|
||||||
$$
|
|
||||||
R_{n}(x_{0})=R'_{n}(x_{0})=...=R^{(n)}_{n}(x_{0})=0
|
|
||||||
$$
|
|
||||||
|
|
||||||
and
|
|
||||||
|
|
||||||
$$
|
|
||||||
Q_{n}(x_{0})=Q'_{n}(x_{0})=...=Q^{(n-1)}_{n}(x_{0})=0 \\ Q^{(n)}_{n}(x_{0})=n!
|
|
||||||
$$
|
|
||||||
|
|
||||||
Because $f^{(n)}(x*{0})$ exists, \
|
|
||||||
Therefore, in a neighborhood $U(x*{0})$ of $x*{0}$, $f(x)$ has a $(n-1)$th order derivative $f^{(n-1)}(x)$. \
|
|
||||||
Thus, when $x\in U^{o}(x*{0})$ and $x\rightarrow x_{0}$, by repeatedly applying L'Hôpital's rule $n-1$ times, we have
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{x \rightarrow x_{0}}{\frac{R_{n}(x)}{Q_{n}(x)}}\\=\lim_{x \rightarrow x_{0}}{\frac{R'_{n}(x)}{Q'_{n}(x)}}\\=...\\=\lim_{x \rightarrow x_{0}}{\frac{R^{(n-1)}_{n}(x)}{Q^{(n-1)}_{n}(x)}}\\=\lim_{x \rightarrow x_{0}}{\frac{f^{(n-1)}(x)-f^{(n-1)}(x_{0})-f^{(n)}(x_{0})(x-x_{0})}{n(n-1)\cdot \cdot \cdot2(x-x_{0})}}\\=\frac{1}{n!}\lim_{x \rightarrow x_{0}}{\left[ \frac{f^{(n-1)}(x)-f^{(n-1)}(x_{0})}{x-x_{0}}-f^{(n)}(x_{0}) \right]}=0
|
|
||||||
$$
|
|
||||||
|
|
||||||
The expression proved by this theorem is termed as the **Taylor formula** for function $f(x)$ at $x_{0}$. Since its corresponding remainder term
|
|
||||||
|
|
||||||
$$
|
|
||||||
R_{n}(x)=f(x)-T_{n}(x)=o((x-x_{0})^{n})
|
|
||||||
$$
|
|
||||||
|
|
||||||
it is also called the **Taylor formula with Peano remainder**. Hence, this expression is also referred to as the **Taylor formula with Peano remainder**.
|
|
||||||
|
|
||||||
**Note:** The Taylor formula (with Peano remainder) is a qualitative expression. Although this expression holds for the entire domain of $f(x)$, its remainder term is meaningful only near the point $x_{0}$. Thus, this expression has strong limitations.
|
|
||||||
|
|
||||||
## Taylor's Theorem
|
|
||||||
|
|
||||||
In order to overcome the drawback of the Taylor formula above, which only allows for a qualitative analysis of functions, we need a more precise quantitative expression to characterize the function $f(x)$. A quantitative expression can more accurately delineate the range of errors when approximating the function $f(x)$ with a polynomial function.
|
|
||||||
|
|
||||||
**Theorem (Taylor's Theorem):** If the function $f(x)$ has continuous derivatives up to $n$th order on $[a, b]$ and has $(n+1)$ st order derivatives on $(a, b)$, then for any given $x, x_{0} \in [a, b]$, there exists at least one point $\xi \in (a, b)$ such that
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+\dots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}
|
|
||||||
$$
|
|
||||||
|
|
||||||
**Analysis:** From the conditions of the theorem, we can see that the functions $f(x)$ and $(x-x_{0})^{n+1}$ can be "arbitrarily" used on $[a, b]$ using the Mean Value Theorem, hence the proof approach utilizes the Mean Value Theorem.
|
|
||||||
|
|
||||||
**Proof:** Let
|
|
||||||
|
|
||||||
$$
|
|
||||||
F(x)=f(x)-[f(x_{0})+f'(x_{0})(x-x_{0})+\dots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}] \\
|
|
||||||
G(x)=(x-x_{0})^{(n+1)} \\
|
|
||||||
x,x_{0}\in[a,b]
|
|
||||||
$$
|
|
||||||
|
|
||||||
To prove
|
|
||||||
|
|
||||||
$$
|
|
||||||
\frac{F(x)}{G(x)}=\frac{f^{(n+1)}(\xi)}{(n+1)!},\xi\in(a,b)
|
|
||||||
$$
|
|
||||||
|
|
||||||
Clearly, $F(x)$ and $G(x)$ both have continuous derivatives up to $n$th order on $[a, b]$ and have $(n+1)$ st order derivatives on $(a, b)$. Also, $F(x_{0})=F'(x_{0})=\dots=F^{(n)}(x_{0})=0$, $G(x_{0})=G'(x_{0})=\dots=G^{(n)}(x_{0})=0$, and $G^{(n+1)}(x)=(n+1)!$. Hence,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\frac{F(x)}{G(x)}=\frac{F(x)-F(x_{0})}{G(x)-G(x_{0})}=\frac{F'(\xi_{1})}{G'(\xi_{1})}=\frac{F'(\xi_{1})-F'(x_{0})}{G'(\xi_{1})-G'(x_{0})}=\frac{F''(\xi_{2})}{G''(\xi_{2})}=\dots \\=\frac{F^{(n)}(\xi_{n})}{G^{(n)}(\xi_{n})}=\frac{F^{(n)}(\xi_{n})-F^{(n)}(x_{0})}{G^{(n)}(\xi_{n})-G^{(n)}(x_{0})}=\frac{F^{(n+1)}(\xi)}{G^{(n+1)}(\xi)}=\frac{f^{(n+1)}(\xi)}{(n+1)!},\xi\in(a,b)
|
|
||||||
$$
|
|
||||||
|
|
||||||
Proof complete.
|
|
||||||
|
|
||||||
**Note:** Taylor's Theorem can be alternatively stated as follows: if $f(x)$ has \((n+1)\)st order derivatives in a neighborhood $U(x_{0})$ of $x_{0}$, then for any point $x$ in this neighborhood, we have
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2} \\+ \dots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1},\xi\in(a,b)
|
|
||||||
$$
|
|
||||||
|
|
||||||
This alternative description may be easier to remember.
|
|
||||||
|
|
||||||
The remainder term
|
|
||||||
|
|
||||||
$$
|
|
||||||
R_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}
|
|
||||||
$$
|
|
||||||
|
|
||||||
is called the **Lagrange remainder**, hence Taylor's Theorem can also be called the **Taylor formula with Lagrange remainder**.
|
|
||||||
|
|
||||||
Furthermore, from the conditions of Taylor's Theorem, it can be seen that the conditions for its use are much stricter compared to the Taylor formula (which only requires $n$th order derivatives to exist at a point $x_{0}$), hence the conclusion obtained is stronger. Taylor's Theorem can be utilized to quantitatively approximate the function $f(x)$ using polynomial functions.
|
|
||||||
|
|
||||||
## Taylor Series
|
|
||||||
|
|
||||||
The Taylor series, compared to the two mathematical concepts mentioned earlier, appeared later in mathematical analysis because it requires a foundation in knowledge of series, power series, and function series. Since the knowledge of series and function series is not the focus of this article, interested readers can refer to any textbook on mathematical analysis for further study. Here, we only provide information closely related to the Taylor series, focusing on power series.
|
|
||||||
|
|
||||||
A power series is a type of function series with the simplest form, generated by the sequence of functions $\left\{ a_{n}(x-x_{0})^{n} \right\}$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}(x-x_{0})^{n}}=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})^{2}+\dots+a_{n}(x-x_{0})^{n}+\dots
|
|
||||||
$$
|
|
||||||
|
|
||||||
To simplify the form, we only discuss the power series when $x_{0}=0$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}=a_{0}+a_{1}x+a_{2}x^{2}+\dots+a_{n}x^{n}+\dots
|
|
||||||
$$
|
|
||||||
|
|
||||||
Correspondingly, by replacing $x$ with $x-x_{0}$, we obtain the general case mentioned above. Hence, the power series mentioned below all refer to the power series:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
When discussing a function series, the first thing we need to know is its domain of convergence. For a power series, its domain of convergence has a special characteristic, as illustrated in the following theorem:
|
|
||||||
|
|
||||||
**Abel's Theorem:** If the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges at $x=\bar{x}\ne0$, then for any $x$ satisfying the inequality $\left| x \right|<\left| \bar{x} \right|$, the power series converges and converges absolutely. If the power series diverges at $x=\bar{x}\ne0$, then for any $x$ satisfying the inequality $\left| x \right|>\left| \bar{x} \right|$, the power series diverges.
|
|
||||||
|
|
||||||
**Proof:** Assume the series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}\bar{x}^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges. By the necessary condition for the convergence of series, the sequence $\left\{ a_{n}\bar{x}^{n} \right\}$ converges to zero and is bounded. Hence, there exists a positive number $M$ such that
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| a_{n}\bar{x}^{n} \right|<M \quad (n=0,1,2,\dots)
|
|
||||||
$$
|
|
||||||
|
|
||||||
Furthermore, for any $x$ satisfying the inequality $\left| x \right|<\left| \bar{x} \right|$, $\left| \frac{x}{\bar{x}} \right|<1$. Thus,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| a_{n}x^{n} \right|=\left| a_{n}\bar{x}^{n}\cdot\frac{x^{n}}{\bar{x}^{n}} \right|=\left| a_{n}\bar{x}^{n} \right|\left| \frac{x}{\bar{x}} \right|^{n}<Mr^{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
where $r=\left| \frac{x}{\bar{x}} \right|<1$. Since the series $\sum_{n=0}^{\infty}{Mr^{n}}$ converges, the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges absolutely when $\left| x \right|<\left| \bar{x} \right|$.
|
|
||||||
|
|
||||||
Conversely, if the power series diverges at $x=\bar{x}\ne0$, and if there exists $x_{0}$ such that $\left| x_{0} \right|>\left| \bar{x} \right|$ and the series $\sum_{n=0}^{\infty}{a_{n}x_{0}^{n}}$ converges, then according to the previous conclusion, the power series should converge absolutely at $x=\bar{x}$, which contradicts the assumption. Thus, for all $x$ satisfying the inequality $\left| x \right|>\left| \bar{x} \right|$, the power series $\sum_{n=0}^{\infty}{a_{n}\bar{x}^{n}}$ diverges.
|
|
||||||
|
|
||||||
In fact, Abel's theorem tells us about the convergence characteristics of power series, that is, the domain of convergence of a power series must be an interval centered at the origin. If we denote the length of this interval as $2R$, then $R$ is called the **radius of convergence** of the power series. We refer to $(-R,R)$ as the **interval of convergence** of the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$.
|
|
||||||
|
|
||||||
**Theorem:** For the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
If $\lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}} = \rho$, then when
|
|
||||||
|
|
||||||
- $(i)$ $0 < \rho < +\infty$, the radius of convergence $R = \frac{1}{\rho}$;
|
|
||||||
- $(ii)$ $\rho = 0$, the radius of convergence $R = +\infty$;
|
|
||||||
- $(iii)$ $p = +\infty$, the radius of convergence $R = 0$.
|
|
||||||
|
|
||||||
**Proof:** For the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{\left| a_{n}x^{n} \right|}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Since
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{n \to \infty}{\sqrt[n]{\left| a_{n}x^{n} \right|}} = \lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}\left| x \right|} = \rho\left| x \right|
|
|
||||||
$$
|
|
||||||
|
|
||||||
According to the root test for positive series, when $\rho\left| x \right| < 1$, $\sum_{n=0}^{\infty}{\left| a_{n}x^{n} \right|}$ converges; when $\rho\left| x \right| > 1$ the power series diverges. Therefore, when $0 < \rho < +\infty$, from $\rho\left| x \right| < 1$, we obtain the radius of convergence $R = \frac{1}{\rho}$. When $\rho = 0$, $\rho\left| x \right| < 1$ holds for any $x$, so $R = +\infty$. When $\rho = +\infty$, $\rho\left| x \right| > 1$ holds for any $x$ except $x = 0$, so $R = 0$.
|
|
||||||
|
|
||||||
**Note:** If
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{n \to \infty}{\frac{\left| a_{n+1} \right|}{\left| a_{n} \right|}} = \rho
|
|
||||||
$$
|
|
||||||
|
|
||||||
then necessarily
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}} = \rho
|
|
||||||
$$
|
|
||||||
|
|
||||||
Therefore, in finding the convergence radius, the ratio test can also be utilized. Additionally, in the above proof, we took the absolute value of each term of the original power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ to obtain the power series $\sum_{n=0}^{\infty}{\left| a_{n}x^{n} \right|}$ for demonstration. Since the power series is absolutely convergent within its convergence interval, these two power series have exactly the same convergence radius. Thus, this proof method is effective.
|
|
||||||
|
|
||||||
Certainly, the method mentioned above for finding the convergence radius has limitations. If the limit $\lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}}$ does not exist (and is not positive infinity), then this method will fail. Therefore, in general mathematical analysis textbooks, a more general method for finding the convergence radius of a power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is given using the method of upper limits. Below is the theorem:
|
|
||||||
|
|
||||||
**(Extended) Theorem:** For the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
If
|
|
||||||
|
|
||||||
$$
|
|
||||||
\varlimsup _{n \rightarrow \infty}{\sqrt[n]{\left| a_{n} \right|}}=\rho
|
|
||||||
$$
|
|
||||||
|
|
||||||
then when
|
|
||||||
|
|
||||||
- $(i)$ $0 < \rho < +\infty$, the radius of convergence $R = \frac{1}{\rho}$;
|
|
||||||
- $(ii)$ $\rho = 0$, the radius of convergence $R = +\infty$;
|
|
||||||
- $(iii)$ $p = +\infty$, the radius of convergence $R = 0$.
|
|
||||||
|
|
||||||
Since this upper limit always exists, any power series can be used to find the convergence radius using this theorem.
|
|
||||||
|
|
||||||
In practical problems of finding the convergence radius of power series, we may encounter "missing term" power series, such as the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{\frac{x^{2n}}{n-3^{2n}}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Such power series can certainly be found using the method of upper limits mentioned above, but a more effective method is to use the root test to deduce the convergence radius of the power series:
|
|
||||||
|
|
||||||
Consider
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{n \rightarrow \infty}{\sqrt[n]{\frac{x^{2n}}{\left| n-3^{2n} \right|}}}=\frac{1}{9}\lim_{n \rightarrow \infty}{\sqrt[n]{\frac{x^{2n}}{1-\frac{n}{3^{2n}}}}}=\frac{x^{2}}{9}
|
|
||||||
$$
|
|
||||||
|
|
||||||
According to the root test for positive series, when $\frac{x^{2}}{9} < 1$, i.e., $\left| x \right| < 3$, the power series converges, and when $\frac{x^{2}}{9} > 1$, i.e., $\left| x \right| > 3$, the power series diverges. When $x = \pm3$, the corresponding series are:
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{\frac{3^{2n}}{n-3^{2n}}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Since
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{n \rightarrow \infty}{\frac{3^{2n}}{n-3^{2n}}}=-1 \neq 0
|
|
||||||
$$
|
|
||||||
|
|
||||||
the series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{\frac{3^{2n}}{n-3^{2n}}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
diverges, indicating that the original series has a convergence interval of $(-3,3)$.
|
|
||||||
|
|
||||||
Power series, compared to general series of functions, exhibit two properties regarding uniform convergence:
|
|
||||||
|
|
||||||
**Property 1:** If the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
has a convergence radius $R (> 0)$, then the power series uniformly converges on its convergence interval \((-R,R)\).
|
|
||||||
|
|
||||||
**Proof:** Let $[a,b]$ be any closed interval within $(-R,R)$, and denote
|
|
||||||
|
|
||||||
$$
|
|
||||||
\bar{x} = \max\left\{ \left| a \right|, \left| b \right| \right\} \in (-R,R)
|
|
||||||
$$
|
|
||||||
|
|
||||||
Then for any point $x$ in $[a,b]$, we have
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| a_{n}x^{n} \right| \leq \left| a_{n}\bar{x}^{n} \right|
|
|
||||||
$$
|
|
||||||
|
|
||||||
Since the power series converges absolutely at the point $\bar{x}$, by the M-test, the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
uniformly converges on $[a,b]$. Since $[a,b]$ was chosen arbitrarily, the power series uniformly converges on the convergence interval $(-R,R)$ .
|
|
||||||
|
|
||||||
**Property 2:** If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ has a convergence radius $R (> 0)$, and converges at $x = R$ (or $x = -R$), then the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ uniformly converges on $[0,R]$ (or $[-R,0]$).
|
|
||||||
|
|
||||||
**Proof:** Suppose the power series converges at $x = R$. For $x \in [0,R]$, we have $\sum_{n=0}^{\infty}{a_{n}x^{n}} = \sum_{n=0}^{\infty}{a_{n}R^{n}(\frac{x}{R})^{n}}$.
|
|
||||||
|
|
||||||
Since the series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}R^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges, and the function sequence
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left\{ (\frac{x}{R})^{n} \right\}
|
|
||||||
$$
|
|
||||||
|
|
||||||
is decreasing and uniformly bounded on $[0,R]$, i.e.,
|
|
||||||
|
|
||||||
$$
|
|
||||||
1 \geq \frac{x}{R} \geq (\frac{x}{R})^{n} \geq ... \geq (\frac{x}{R})^{n} \geq ... \geq 0
|
|
||||||
$$
|
|
||||||
|
|
||||||
by Abel's test, the series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
uniformly converges on $[0,R]$.
|
|
||||||
|
|
||||||
**Note:** In fact, since the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is uniformly convergent on $(-R,0]$ , the conclusion can also be drawn: when the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges at $x = R$, the power series uniformly converges on $(-R,R]$.
|
|
||||||
|
|
||||||
From the two properties regarding uniform convergence of power series, we can deduce other properties that power series possess:
|
|
||||||
|
|
||||||
$(i)$ The sum function of the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is continuous on \((-R,R)\).
|
|
||||||
|
|
||||||
$(ii)$ If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges at the left (right) endpoint of its convergence interval, then its sum function is also continuous at this endpoint from the right (left).
|
|
||||||
|
|
||||||
**Note:** Since each term of the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is continuous on \((-R,R)\), and $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ uniformly converges on \((-R,R)\), we can deduce property $(i)$ from the properties of uniform convergence of series of functions. If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges at $x = R$ (or $x = -R$), then the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ uniformly converges on $[0,R]$ (or $[-R,0]$) by the same reasoning, thus property $(ii)$ holds.
|
|
||||||
|
|
||||||
In the study of series of functions, there are theorems concerning term-by-term integration and differentiation:
|
|
||||||
|
|
||||||
**(Term-by-term Integration Theorem):** If the series of functions
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
|
||||||
$$
|
|
||||||
|
|
||||||
uniformly converges on $[a,b]$, and each term $u_{n}(x)$ is continuous, then
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{\int_{a}^{b}u_{n}(x)dx}=\int_{a}^{b}\sum_{n=0}^{\infty}{u_{n}(x)dx}
|
|
||||||
$$
|
|
||||||
|
|
||||||
**(Term-by-term Differentiation Theorem):** If the series of functions
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
|
||||||
$$
|
|
||||||
|
|
||||||
has continuous derivative for each term on $[a,b]$, $x_{0}\in[a,b]$ is a point of convergence for
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
|
||||||
$$
|
|
||||||
|
|
||||||
, and
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{u'_{n}(x)}
|
|
||||||
$$
|
|
||||||
|
|
||||||
uniformly converges on $[a,b]$, then
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}({\frac{d}{dx}u_{n}(x)})=\frac{d}{dx}(\sum_{n=0}^{\infty}{u_{n}(x)})
|
|
||||||
$$
|
|
||||||
|
|
||||||
**Note:** The requirement that $x_{0}\in[a,b]$ is a point of convergence for
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
|
||||||
$$
|
|
||||||
|
|
||||||
in the term-by-term differentiation theorem is for the convenience of application. Its equivalent condition is that
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges on $[a,b]$. Furthermore, the interval $[a,b]$ in the conditions can be replaced with a general open interval, and the conclusion still holds.
|
|
||||||
|
|
||||||
For the power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
its power series obtained by differentiating each term is
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{na_{n}x^{n-1}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
and the power series obtained by integrating each term is
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{\frac{a_{n}x^{n+1}}{n+1}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
For convenience, let's denote the three power series as $(1)$, $(2)$, and $(3)$, respectively.
|
|
||||||
|
|
||||||
To discuss term-by-term differentiation and integration of power series, we first introduce the following lemma:
|
|
||||||
|
|
||||||
**Lemma:** Power series $(1)$ and $(2)$, $(3)$ have the same interval of convergence.
|
|
||||||
|
|
||||||
**Proof:** We only need to prove that $(1)$ and $(2)$ have the same interval of convergence because differentiating each term of $(3)$ results in $(2)$.
|
|
||||||
|
|
||||||
Suppose $(1)$ converges only at $x=0$. Assuming $(2)$ converges at $x'>0$, then for $\bar{x}\in(0,x')$, by the Abel's theorem,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{\left| na_{n}\bar{x}^{n-1} \right|}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges. Thus,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| a_{n}\bar{x}^{n}\right|=\left| na_{n}\bar{x}^{n-1} \right|\left| \frac{\bar{x}}{n} \right|=\left| na_{n}\bar{x}^{n-1} \right|\frac{\bar{x}}{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
Since it is given that
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{\left| na_{n}\bar{x}^{n-1} \right|}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left\{ \frac{\bar{x}}{n} \right\}
|
|
||||||
$$
|
|
||||||
|
|
||||||
is monotonically bounded. Thus, by the Abel's test, we know that
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=1}^{\infty}{\left| a_{n}\bar{x}^{n} \right|}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges. This contradicts the assumption. Therefore, $(2)$ also converges only at $x=0$, and the proposition holds.
|
|
||||||
|
|
||||||
Now let the convergence interval of power series $(1)$ be $(-R,R)$, where $R\neq 0$. Let $x_{0}$ be any nonzero point in $(-R,R)$. As shown in the proof of the Abel's theorem, there exist positive numbers $M$ and $r(0<r<1)$ such that for all positive integers $n$,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| a_{n}x_{0}^{n} \right|<Mr^{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
So,
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| na_{n}x_{0}^{n-1} \right|=\left| \frac{n}{x_{0}} \right|\left| a_{n}x_{0}^{n} \right|<\frac{M}{\left| x_{0} \right|}nr^{n}
|
|
||||||
$$
|
|
||||||
|
|
||||||
By the ratio test, the series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{nr^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges. Therefore, by the comparison test, the series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{\left| na_{n}x_{0}^{n-1} \right|}
|
|
||||||
$$
|
|
||||||
|
|
||||||
converges. This implies that power series $(2)$ is absolutely convergent (and hence convergent) at point $x_{0}$, as it converges absolutely. Since $x_{0}$ is an arbitrary point in $(-R,R)$, power series $(2)$ converges on the interval $(-R,R)$.
|
|
||||||
|
|
||||||
Next, we need to prove that power series $(2)$ does not converge for all $x$ satisfying $\left| x \right|>R$. Suppose $(2)$ converges at a point $x_{0} (\left| x_{0} \right|>R)$, then there exists a number $\bar{x}$ such that $\left| x_{0} \right|>\left| \bar{x} \right|>R$. By the Abel's theorem, power series $(2)$ converges absolutely at $x=\bar{x}$. However, when $n\geq\left| \bar{x} \right|$, we have
|
|
||||||
|
|
||||||
$$
|
|
||||||
\left| na_{n}\bar{x}^{n-1} \right|=\frac{n}{\left| \bar{x} \right|}\left| a_{n}\bar{x}^{n} \right|\geq \left| a_{n}\bar{x}^{n} \right|
|
|
||||||
$$
|
|
||||||
|
|
||||||
By the comparison test, power series $(1)$ converges absolutely at $x=\bar{x}$. This contradicts the fact that the convergence interval of power series $(1)$ is $(-R,R)$. Thus, power series $(2)$ does not converge for all $x$ satisfying $\left| x \right|>R$. In summary, power series $(1)$ and $(2)$ have the same interval of convergence.
|
|
||||||
|
|
||||||
Regarding term-by-term differentiation and integration of power series, we have the following theorem:
|
|
||||||
|
|
||||||
**Theorem:** Suppose the convergence interval of series $(1)$ is $(-R, R)$, and its sum function on this interval is denoted by $f(x)$. If $x$ is any point in $(-R, R)$, then:
|
|
||||||
|
|
||||||
- $(i)$ $f(x)$ is differentiable at point $x$, and
|
|
||||||
$$
|
|
||||||
f'(x)=\sum_{n=1}^{\infty}{na_{n}x^{n-1}}
|
|
||||||
$$
|
|
||||||
- $(ii)$ $f(x)$ is integrable over the interval between $0$ and $x$ on $(-R, R)$, and
|
|
||||||
$$
|
|
||||||
\int_{0}^{x}f(t)dt=\sum_{n=0}^{\infty}{\frac{a_{n}}{n+1}x^{n+1}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
**Proof:** Since series $(1)$, $(2)$, and $(3)$ have the same convergence radius $R$, and each term of series $(1)$ has a continuous derivative, and all three power series converge uniformly on the closed interval $(-R, R)$, they satisfy the theorem of term-by-term differentiation and integration of function series. Therefore, the above theorem holds.
|
|
||||||
|
|
||||||
From the above theorem, we can derive the following corollaries:
|
|
||||||
|
|
||||||
**Corollary 1:** Let $f(x)$ be the sum function of series $(1)$ on the convergence interval $(-R, R)$. Then, $f(x)$ has derivatives of any order on $(-R, R)$, and can be differentiated term by term any number of times, i.e.,
|
|
||||||
|
|
||||||
$$
|
|
||||||
f'(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+...+na_{n}x^{n-1}+...
|
|
||||||
$$
|
|
||||||
|
|
||||||
$$
|
|
||||||
f''(x)=2a_{2}+3\cdot2a_{3}x+...+n(n-1)a_{n}x^{n-2}+...
|
|
||||||
$$
|
|
||||||
|
|
||||||
$$
|
|
||||||
f^{(n)}(x)=n!a_{n}+(n+1)n(n-1)...2a_{n+1}x+...
|
|
||||||
$$
|
|
||||||
|
|
||||||
**Corollary 2:** Let $f(x)$ be the sum function of series $(1)$ on the convergence interval $(-R, R)$. Then the coefficients of series $(1)$ are determined by the various derivatives of $f(x)$ at $x=0$:
|
|
||||||
|
|
||||||
$$
|
|
||||||
a_{0}=f(0) \\ a_{n}=\frac{f^{(n)}(0)}{n!} \quad (n=1,2,...)
|
|
||||||
$$
|
|
||||||
|
|
||||||
**Equality of Power Series:** If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ and $\sum_{n=0}^{\infty}{b_{n}x^{n}}$ have the same sum function in a neighborhood of $x=0$, then these two power series are considered equal in that neighborhood.
|
|
||||||
|
|
||||||
Since the coefficients of power series are determined by the sum function and its derivatives at $x=0$, it follows from the definition of equality of power series that two power series are equal in a neighborhood if and only if their coefficients are equal.
|
|
||||||
|
|
||||||
**Arithmetic Operations on Power Series:** Suppose the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ and $\sum_{n=0}^{\infty}{b_{n}x^{n}}$ have convergence radii $R_{a}$ and $R_{b}$, respectively. Then:
|
|
||||||
|
|
||||||
- $(i)$ $\lambda\sum_{n=0}^{\infty}{a_{n}x^{n}}=\sum_{n=0}^{\infty}{\lambda a_{n}x^{n}},\left| x \right|<R$ ;
|
|
||||||
- $(ii)$ $\sum_{n=0}^{\infty}{a_{n}x^{n}}\pm\sum_{n=0}^{\infty}{b_{n}x^{n}}=\sum_{n=0}^{\infty}{(a_{n}\pm b_{n})x^{n}},\left| x \right|<R$ ;
|
|
||||||
- $(iii)$ $(\sum_{n=0}^{\infty}{a_{n}x^{n}})(\sum_{n=0}^{\infty}{b_{n}x^{n}})=\sum_{n=0}^{\infty}{c_{n}x^{n}},\left| x \right|<R$ .
|
|
||||||
|
|
||||||
where $\lambda$ is a constant, and $R=\min\{ R_{a}, R_{b} \}$, $c_{n}=\sum_{k=0}^{n}{a_{k}b_{n-k}}$.
|
|
||||||
|
|
||||||
These properties can be derived from the corresponding properties of numerical series.
|
|
||||||
|
|
||||||
The above discussion regarding power series actually serves as a preliminary study for Taylor series. Although it might seem extensive, it's essential for understanding Taylor series thoroughly.
|
|
||||||
|
|
||||||
In the section on Taylor's theorem, we previously mentioned that if a function $f(x)$ has derivatives up to order $n + 1$ in a neighborhood of $x_{0}$, then the Taylor series expansion is given by:
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x) = f(x_{0}) + f'(x_{0})(x-x_{0}) + \frac{f''(x_{0})}{2!}(x-x_{0})^{2} + \ldots + \frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n} + R_{n}(x)
|
|
||||||
$$
|
|
||||||
|
|
||||||
Here, $R_{n}(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}$, where $\xi$ lies between $x$ and $x_{0}$.
|
|
||||||
|
|
||||||
Inspired by the form of Taylor's theorem, if a function $f(x)$ has derivatives of all orders at $x = x_{0}$, then we can construct a power series:
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x_{0}) + f'(x_{0})(x-x_{0}) + \frac{f''(x_{0})}{2!}(x-x_{0})^{2} + \ldots + \frac{f^{(n)}(x-x_{0})^{n}}{n!} + \ldots
|
|
||||||
$$
|
|
||||||
|
|
||||||
This series is called the **Taylor series** of the function $f(x)$ at the point $x_{0}$. Now, we face the question: What is the relationship between the function $f(x)$ and its Taylor series expansion at $x_{0}$? If the function $f(x)$ is defined in a neighborhood $U(x_{0},\delta)$ and its Taylor series converges in the interval $U(x_{0},R)$, does the function $f(x)$ equal the sum function of its Taylor series in $U(x_{0},\delta)\cap U(x_{0},R)$?
|
|
||||||
|
|
||||||
**Theorem:** Suppose $f(x)$ has derivatives of all orders at the point $x_{0}$. Then, $f(x)$ equals the sum function of its Taylor series on the interval $(x_{0}-r,x_{0}+r)$ if and only if, for all $x$ satisfying $|x-x_{0}|<r$, we have
|
|
||||||
|
|
||||||
$$
|
|
||||||
\lim_{n \rightarrow \infty}{R_{n}(x)} = 0
|
|
||||||
$$
|
|
||||||
|
|
||||||
Here, $R_{n}(x)$ represents the Lagrange remainder term of $f(x)$ at $x_{0}$.
|
|
||||||
|
|
||||||
**Proof:** Given that $f(x)$ has derivatives of all orders at $x_{0}$, by Taylor's theorem, for any $x \in U(x_{0},r)$, where $r \leq R$, we have $f(x) = T_{n}(x) + R_{n}(x)$.
|
|
||||||
|
|
||||||
**[Necessity]:** If $f(x) = \lim_{n \rightarrow \infty}{T_{n}(x)}$, then as $n \rightarrow \infty$, we have $\lim_{n \rightarrow \infty}{R_{n}(x)} = 0$.
|
|
||||||
|
|
||||||
**[Sufficiency]:** If $\lim_{n \rightarrow \infty}{R_{n}(x)} = 0$, then $f(x) = \lim_{n \rightarrow \infty}{T_{n}(x)}$.
|
|
||||||
|
|
||||||
## Taylor Expansion
|
|
||||||
|
|
||||||
If function $f(x)$ can be expressed as the sum function of its Taylor series in a neighborhood of point $x*{0}$, then function $f(x)$ can be expanded into a Taylor series in the neighborhood of point $x*{0}$. The right side of the equation
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+...+\frac{f^{(n)}(x_{0})^{n}}{n!}+...
|
|
||||||
$$
|
|
||||||
|
|
||||||
is called the **Taylor expansion** of $f(x)$ at point $x_{0}$.
|
|
||||||
|
|
||||||
According to the previous theorem, if function $f(x)$ is the sum function of a power series
|
|
||||||
|
|
||||||
$$
|
|
||||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
|
||||||
$$
|
|
||||||
|
|
||||||
in the convergence interval $(-R, R)$, then the coefficients of $\sum*{n=0}^{\infty}{a*{n}x^{n}}$ are determined by the sum function $f(x)$ and the values of its various order derivatives at $x=0$, that is,
|
|
||||||
|
|
||||||
$$
|
|
||||||
a_{0}=f(0) \\ a_{n}=\frac{f^{(n)}(0)}{n!} \\ n=1,2,...
|
|
||||||
$$
|
|
||||||
|
|
||||||
That is, $\sum*{n=0}^{\infty}{a*{n}x^{n}}$ is the Taylor expansion of function $f(x)$ on $(-R, R)$.
|
|
||||||
|
|
||||||
The above is the process of analyzing these four mathematical concepts. In the part of Taylor series, the relevant concepts of power series are elaborated in detail. Here we summarize these four concepts:
|
|
||||||
|
|
||||||
**Summary:** From the chronological point of view, we usually encounter the Taylor formula for the first time in the part of the mean value theorem of differentiation in the first volume of mathematical analysis, that is, the Taylor formula with the Peano remainder term, which is introduced by the finite increment formula in the derivative:
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})
|
|
||||||
$$
|
|
||||||
|
|
||||||
When using the finite increment formula for estimation, the error is $o(x-x*{0})$, and its estimation effect is quite rough. If the function is known to have an $n$-th order derivative at the point $x*{0}$, we can generalize the finite increment formula, that is, to obtain the Taylor formula with the Peano remainder term. Its estimation error is $o((x-x*{0})^{n})$. In order to further improve the estimation effect and quantitatively analyze the range of errors, the Taylor formula with the Lagrange remainder term is introduced. The use condition of Taylor formula with the Lagrange remainder term is further strict, which requires that the function $f(x)$ has derivatives up to $(n+1)$-th order at the point $x*{0}$. Its corresponding error is
|
|
||||||
|
|
||||||
$$
|
|
||||||
\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}
|
|
||||||
$$
|
|
||||||
|
|
||||||
The Lagrange remainder term can quantitatively analyze the error, and its estimation effect is much better than that of the Peano remainder term.
|
|
||||||
|
|
||||||
Following the learning order of the textbook, after learning related knowledge such as series, functional series, and power series in the second volume of mathematical analysis, we can introduce the concept of Taylor series. If the function $f(x)$ has derivatives of any order at some point $x_{0}$, then we can write
|
|
||||||
|
|
||||||
$$
|
|
||||||
f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+...+\frac{f^{(n)}(x_{0})^{n}}{n!}+...
|
|
||||||
$$
|
|
||||||
|
|
||||||
This expression is called the Taylor series of function $f(x)$ at point $x*{0}$. As a special power series, the Taylor series has a convergence range, namely the convergence domain of the Taylor series, and we give the necessary and sufficient conditions for the Taylor series of function $f(x)$ at point $x*{0}$ in a certain neighborhood $U(x*{0},r)$ to be equal to its sum function: $\lim*{n \rightarrow \infty}{R_{n}(x)}=0$.
|
|
||||||
|
|
||||||
This leads to the concept of Taylor expansion. The so-called Taylor expansion refers to the power series expression that function $f(x)$ can be expanded into in a certain neighborhood. In this neighborhood, function $f(x)$ is completely characterized by the power series. This is different from the approximation by polynomial functions above, but is equal in a real sense. However, the application of power series has certain limitations, namely, because the convergence domain of power series is often a finite interval, it can only characterize function $f(x)$ in a small segment interval. In order to solve this drawback of power series, research on Fourier series has emerged.
|
|
||||||
@@ -1,195 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Data Table Relation's Normalization"
|
|
||||||
subtitle: ""
|
|
||||||
summary: "Introduces functional dependencies, and the database paradigms 1NF, 2NF, 3NF, BCNF, and 4NF. and use examples to explain their concepts and connections."
|
|
||||||
coverURL: ""
|
|
||||||
time: "2024-03-12"
|
|
||||||
tags: ["database"]
|
|
||||||
noPrompt: false
|
|
||||||
pin: false
|
|
||||||
allowShare: true
|
|
||||||
---
|
|
||||||
|
|
||||||
## Functional Dependencies
|
|
||||||
|
|
||||||
In relational databases, functional dependencies describe the dependency relationships between attributes in a relational schema. If, given a relation $R$, the values of attribute set $X$ uniquely determine (through conditions or function arguments, for example) a value in attribute set $Y$, then we say that $Y$ is functionally dependent on $X$, typically denoted by the symbol $X \rightarrow Y$.
|
|
||||||
|
|
||||||
Specifically, if for every record in relation $R$, whenever two records have the same values for attribute set $X$, they must also have the same values for attribute set $Y$, then we say that $Y$ is functionally dependent on $X$.
|
|
||||||
|
|
||||||
For example, suppose we have a relation $R$ containing attribute set $\{ A,B,C \}$, where the values of attribute $A$ uniquely determine the values of attribute $B$, i.e., $A \rightarrow B$. Then, we say that attribute $B$ is functionally dependent on attribute $A$.
|
|
||||||
|
|
||||||
Functional dependency is an important concept in relational database design. It helps in understanding the relationships between data, normalizing database designs to reduce redundant data, while ensuring the consistency and integrity of data.
|
|
||||||
|
|
||||||
Functional dependencies can be classified into trivial functional dependencies and non-trivial functional dependencies.
|
|
||||||
|
|
||||||
If $X \rightarrow Y$ and $Y \subseteq X$, then $X \rightarrow Y$ is called a trivial functional dependency. Otherwise, it is a non-trivial functional dependency.
|
|
||||||
|
|
||||||
For functional dependencies, the dependency relationship between $X$ and $Y$ can also be further classified into partial functional dependency, full functional dependency, and transitive functional dependency.
|
|
||||||
|
|
||||||
- Partial Functional Dependency: Let $X,Y$ be two attribute sets of relation $R$. If $X→Y$ and $X' \subsetneq X$, where there exists $X'$ such that $X'→Y$, then $Y$ is said to be partially functionally dependent on $X$, denoted as $X \overset{P}{\rightarrow} Y$. In other words, partial functional dependency means that some attributes can be removed without affecting the dependency.
|
|
||||||
|
|
||||||
> For example: In a student basic information table $R$ (student ID, passport number, name), of course, the student ID attribute values are unique. In relation $R$, (student ID, passport number) → (name), (student ID) → (name), (passport number) → (name); therefore, the name is partially functionally dependent on (student ID, passport number).
|
|
||||||
|
|
||||||
- Full Functional Dependency: Let $X,Y$ be two attribute sets of relation $R$. If $X→Y$, $X' \subsetneq X$, and for all $X'$, $X'→Y$, then $Y$ is said to be fully functionally dependent on $X$, denoted as $X \overset{F}{\rightarrow} Y$. In other words, for full functional dependency, no extra attributes can be deleted, otherwise, the property of dependency will not be maintained.
|
|
||||||
|
|
||||||
> Example: In a student basic information table $R$ (student ID, class, name), assuming different classes can have the same student ID, and student IDs within a class cannot be the same. In relation $R$, (student ID, class) → (name), but (student ID) → (name) does not hold, and (class) → (name) does not hold either. Therefore, the name is fully functionally dependent on (student ID, class).
|
|
||||||
|
|
||||||
- Transitive Functional Dependency: Let $X,Y,Z$ be three attribute sets of relation $R$, where $X→Y (Y \cancel{\rightarrow} X)$, and for all $Y$, $Y→Z$. Then $Z$ is said to be transitively functionally dependent on $X$. This means that $Z$ indirectly depends on $X$.
|
|
||||||
|
|
||||||
> Example: In relation $R$ (student ID, dormitory, fee), (student ID) → (dormitory), dormitory ≠ student ID, (dormitory) → (fee), fee ≠ dormitory. Thus, it meets the requirements of transitive functional dependency.
|
|
||||||
|
|
||||||
## Multi-Valued Dependencies
|
|
||||||
|
|
||||||
The previous section introduced functional dependencies, which are actually a special case of multi-valued dependencies. Multi-valued dependencies extend the concept of functional dependencies.
|
|
||||||
|
|
||||||
Let $R(U)$ be a relational schema over the attribute set $U$, and let $X$, $Y$, and $Z$ be subsets of $U$ such that $Z = U - X - Y$. A multi-valued dependency $X \twoheadrightarrow Y$ holds if and only if for any relation $r$ in $R$, each value on $(X, Z)$ corresponds to a set of values on $Y$, and this set of values depends only on the values of $X$ and is independent of the values of $Z$.
|
|
||||||
|
|
||||||
Consider a relational schema $R$ with the attribute set $\{Student, Course, Textbook\}$, representing students' course enrollments and the textbooks they use. If a student uses multiple textbooks for a single course, and the combination of student and course uniquely determines the textbooks used, while the combination of student and course is independent, then we have a multi-valued dependency.
|
|
||||||
|
|
||||||
Suppose we have the following relation instance:
|
|
||||||
|
|
||||||
| Student | Course | Textbook |
|
|
||||||
| ------- | ------- | -------------- |
|
|
||||||
| Alice | Math | Calculus |
|
|
||||||
| Alice | Math | Linear Algebra |
|
|
||||||
| Alice | Physics | Mechanics |
|
|
||||||
| Bob | Math | Calculus |
|
|
||||||
|
|
||||||
In this example, the choice of textbook depends on the combination of student and course. For instance, Alice uses both Calculus and Linear Algebra textbooks for her Math course, while she uses Mechanics for her Physics course. However, whether Linear Algebra and Calculus are chosen depends solely on whether the course is Math.
|
|
||||||
This scenario demonstrates a multi-valued dependency, where the combination of student and course uniquely determines the set of textbooks used, while the relationship between student and course is independent, yet textbooks are not independent of courses as one course can have multiple textbooks.
|
|
||||||
|
|
||||||
Therefore, in this scenario, there exists a multi-valued dependency relationship $Course \twoheadrightarrow Textbook$.
|
|
||||||
|
|
||||||
## Keys
|
|
||||||
|
|
||||||
- Let $K$ be an attribute or a combination of attributes in $R<U, F>$, and $K \overset{F}{\rightarrow} U$, then $K$ is a candidate key for $R$.
|
|
||||||
- If there are multiple candidate keys, one of them can be designated as the primary key.
|
|
||||||
- Any attribute set that contains a candidate key is called a prime attribute. Otherwise, it is a non-prime attribute.
|
|
||||||
- If the entire attribute set constitutes the candidate key, then this attribute set is called a superkey.
|
|
||||||
- Both primary keys and candidate keys are commonly referred to as keys.
|
|
||||||
|
|
||||||
## Database Normalization
|
|
||||||
|
|
||||||
### 1NF
|
|
||||||
|
|
||||||
$1NF$ (First Normal Form) is one of the fundamental normal forms in relational databases. It requires that each attribute in a relation schema is atomic, meaning it cannot be further divided. In other words, each attribute in the relation schema should be single-valued, rather than containing multiple values or complex data types.
|
|
||||||
|
|
||||||
Specifically, $1NF$ requires that each cell in the relation contains only one value, rather than multiple values or complex data types. This helps ensure the atomicity of data, simplifying data processing and querying.
|
|
||||||
|
|
||||||
For example, consider a student table containing names and phone numbers. If phone numbers are stored as a comma-separated list of multiple numbers, then this table does not conform to $1NF$. To adhere to $1NF$, phone numbers should be split into separate attributes, with each attribute containing only one phone number.
|
|
||||||
|
|
||||||
### 2NF
|
|
||||||
|
|
||||||
$2NF$ (Second Normal Form) is another normal form in relational databases, built upon the foundation of the first normal form ($1NF$). $2NF$ requires that each non-prime attribute in a relation schema is fully functionally dependent on the candidate key, rather than partially dependent on the candidate key.
|
|
||||||
|
|
||||||
Specifically, if a relation schema has multiple attributes forming the candidate key, then each non-prime attribute should depend on all combinations of these attributes, rather than just depending on some of them.
|
|
||||||
|
|
||||||
For example, consider a relation schema containing the following attributes: StudentID, CourseID, CourseName, StudentName, and Grade. In this schema, (StudentID, CourseID) forms the candidate key, representing the enrollment of students in courses.
|
|
||||||
|
|
||||||
| StudentID | CourseID | CourseName | StudentName | Grade |
|
|
||||||
| --------- | -------- | ---------- | ----------- | ----- |
|
|
||||||
| 101 | 001 | Math | Alice | A |
|
|
||||||
| 101 | 002 | Physics | Alice | B |
|
|
||||||
| 102 | 001 | Math | Bob | A |
|
|
||||||
| 102 | 003 | Chemistry | Bob | C |
|
|
||||||
|
|
||||||
In this example, the StudentName attribute is a non-prime attribute and is partially dependent on the candidate key (StudentID), rather than fully dependent on all attributes of the candidate key (StudentID, CourseID). For instance, the name of student Alice is only associated with Student ID 101, irrespective of the course enrollment.
|
|
||||||
|
|
||||||
Therefore, this relation schema does not satisfy the second normal form ($2NF$). To adhere to $2NF$, we should remove the StudentName attribute from this relation schema and place it in a separate table, where the candidate key is $StudentID$. This way, the student name becomes fully dependent on the candidate key, rather than partially dependent on it.
|
|
||||||
|
|
||||||
### 3NF
|
|
||||||
|
|
||||||
Given a relation schema $R<U,F> \in 1NF$ and no set of attributes $X$, attribute group $Y$, and non-candidate attribute $Z$ such that $X \rightarrow Y, Y \rightarrow Z, Y \cancel{\rightarrow} X$, it belongs to $3NF$. In other words, if a relation is in $2NF$ and each non-candidate attribute does not transitively depend on the candidate key, then it is in $3NF$.
|
|
||||||
|
|
||||||
Let's continue with the example of student course enrollment mentioned earlier and attempt to conform to the third normal form ($3NF$).
|
|
||||||
|
|
||||||
In this example, we have already removed the student name from the main table and placed it in a separate table as follows:
|
|
||||||
|
|
||||||
**Student Table**:
|
|
||||||
|
|
||||||
| StudentID | StudentName |
|
|
||||||
| --------- | ----------- |
|
|
||||||
| 101 | Alice |
|
|
||||||
| 102 | Bob |
|
|
||||||
|
|
||||||
**Enrollment Table**:
|
|
||||||
|
|
||||||
| StudentID | CourseID | Grade |
|
|
||||||
| --------- | -------- | ----- |
|
|
||||||
| 101 | 001 | A |
|
|
||||||
| 101 | 002 | B |
|
|
||||||
| 102 | 001 | A |
|
|
||||||
| 102 | 003 | C |
|
|
||||||
|
|
||||||
Now, let's see if it conforms to $3NF$. In this relation schema, we have a transitive dependency: Student ID (StudentID) determines Student Name (StudentName), while Course ID (CourseID) determines Student ID (StudentID). Hence, there exists a transitive functional dependency: $CourseID \rightarrow StudentName$.
|
|
||||||
|
|
||||||
To conform to $3NF$, we need to eliminate this transitive dependency. One way to do this is by creating a new table that maps $CourseID$ and $StudentID$ to $StudentName$ to eliminate this transitive dependency. This way, we can ensure that each non-prime attribute is fully dependent on the primary key.
|
|
||||||
|
|
||||||
**Student Enrollment Relation Table**:
|
|
||||||
|
|
||||||
| StudentID | CourseID | Grade |
|
|
||||||
| --------- | -------- | ----- |
|
|
||||||
| 101 | 001 | A |
|
|
||||||
| 101 | 002 | B |
|
|
||||||
| 102 | 001 | A |
|
|
||||||
| 102 | 003 | C |
|
|
||||||
|
|
||||||
**Student Table**:
|
|
||||||
|
|
||||||
| StudentID | StudentName |
|
|
||||||
| --------- | ----------- |
|
|
||||||
| 101 | Alice |
|
|
||||||
| 102 | Bob |
|
|
||||||
|
|
||||||
**Course Table**:
|
|
||||||
|
|
||||||
| CourseID | CourseName |
|
|
||||||
| -------- | ----------- |
|
|
||||||
| 001 | Mathematics |
|
|
||||||
| 002 | Physics |
|
|
||||||
| 003 | Chemistry |
|
|
||||||
|
|
||||||
Now, each table conforms to the third normal form ($3NF$). The student table and the course table are associated with the student enrollment relation table without any transitive dependency.
|
|
||||||
|
|
||||||
### BCNF
|
|
||||||
|
|
||||||
$BCNF$ (Boyce-Codd Normal Form) is a more stringent form of normalization in relational databases, resulting from normalizing relation schemas further from the third normal form ($3NF$). $BCNF$ requires that every non-trivial functional dependency (non-trivial $X \rightarrow Y$, where $Y$ is not a superset of $X$) is determined by the keys of the relation.
|
|
||||||
|
|
||||||
In other words, if $R$ is a relation schema and $X \rightarrow Y$ is a non-trivial functional dependency of $R$, and $X$ does not contain any candidate keys, then $R$ does not conform to $BCNF$, meaning every determinant must include a key.
|
|
||||||
|
|
||||||
For example, consider a scheduling table now, recording student ID, course ID, and teacher ID. A teacher teaches only one course, and a course can be taught by multiple teachers, and each student selects a specific course, which corresponds to a fixed teacher. Assuming the candidate key is student ID, course ID. We can list the following functional relationships:
|
|
||||||
|
|
||||||
- $(StudentID,CourseID) \rightarrow TeacherID$
|
|
||||||
- $(StudentID,TeacherID) \rightarrow CourseID$
|
|
||||||
- $TeacherID \rightarrow CourseID$
|
|
||||||
|
|
||||||
This relation does not conform to $BCNF$ because we find that in the third functional dependency, $TeacherID$ does not contain any keys. While the first and second have keys.
|
|
||||||
|
|
||||||
### 4NF
|
|
||||||
|
|
||||||
$4NF$ is a form of database normalization that further emphasizes the elimination of multi-valued dependencies on top of $BCNF$. A relation schema satisfies $4NF$ if, in addition to satisfying the requirements of $BCNF$, it also has no non-trivial multi-valued dependencies. Non-trivial multi-valued dependencies refer to those where neither the left side nor the right side is a superkey of the relation.
|
|
||||||
|
|
||||||
Let's consider an example that complies with $BCNF$ but not with $4NF$.
|
|
||||||
|
|
||||||
Suppose we have a relation schema $R$ containing attributes: Student, Course, Grade, and Teacher. And there exist the following functional dependencies:
|
|
||||||
|
|
||||||
1. $(Student, Course) \rightarrow Grade$
|
|
||||||
2. $Course \rightarrow Teacher$
|
|
||||||
3. $Student \twoheadrightarrow Teacher$
|
|
||||||
|
|
||||||
Assume that the candidate key for the relation schema is $Student, Course$.
|
|
||||||
|
|
||||||
This schema conforms to $BCNF$ because every functional dependency is determined by the candidate key.
|
|
||||||
|
|
||||||
However, it does not conform to $4NF$ due to the presence of the third multi-valued dependency. This is because each student may attend multiple courses, and each course may have different teachers.
|
|
||||||
|
|
||||||
Therefore, although this relation schema satisfies $BCNF$, it does not satisfy $4NF$.
|
|
||||||
|
|
||||||
### Relationship
|
|
||||||
|
|
||||||
Understanding from $1NF$ to $4NF$ is progressive. The relationship between them is as follows:
|
|
||||||
|
|
||||||
- $1NF$ eliminates partial functional dependencies of non-prime attributes on the candidate key to achieve $2NF$.
|
|
||||||
- $2NF$ eliminates transitive functional dependencies of non-prime attributes on the candidate key to achieve $3NF$.
|
|
||||||
- $3NF$ eliminates partial and transitive functional dependencies of prime attributes on the candidate key to achieve $BCNF$.
|
|
||||||
- $BCNF$ eliminates non-trivial and functional dependencies of multi-valued dependencies to achieve $4NF$.
|
|
||||||
@@ -1,246 +0,0 @@
|
|||||||
---
|
|
||||||
title: "Chinese-Japanese-Korean Characters Typography Preview"
|
|
||||||
subtitle: ""
|
|
||||||
summary: "This article is used to display fonts, typography and layout effects for Chinese, Japanese and Korean characters."
|
|
||||||
coverURL: ""
|
|
||||||
time: "2024-02-17"
|
|
||||||
tags: ["others"]
|
|
||||||
noPrompt: false
|
|
||||||
pin: false
|
|
||||||
allowShare: true
|
|
||||||
closed: false
|
|
||||||
---
|
|
||||||
|
|
||||||
## 独立宣言(简体中文)
|
|
||||||
|
|
||||||
在人类事务发展的过程中,当一个民族必须解除同另一个民族的联系,并按照自然法则和上帝的旨意,以独立平等的身份立于世界列国之林时,出于对人类舆论的尊重,必须把驱使他们独立的原因予以宣布。
|
|
||||||
|
|
||||||
我们认为下述真理是不言而喻的:人人生而平等,造物主赋予他们若干不可让与的权利,其中包括生存权、自由权和追求幸福的权利。为了保障这些权利,人们才在他们中间建立政府,而政府的正当权利,则是经被统治者同意授予的。任何形式的政府一旦对这些目标的实现起破坏作用时,人民便有权予以更换或废除,以建立一个新的政府。新政府所依据的原则和组织其权利的方式,务使人民认为唯有这样才最有可能使他们获得安全和幸福。若真要审慎的来说,成立多年的政府是不应当由于无关紧要的和一时的原因而予以更换的。过去的一切经验都说明,任何苦难,只要尚能忍受,人类还是情愿忍受,也不想为申冤而废除他们久已习惯了的政府形式。然而,当始终追求同一目标的一系列滥用职权和强取豪夺的行为表明政府企图把人民至于专制暴政之下时,人民就有权也有义务去推翻这样的政府,并为其未来的安全提供新的保障。这就是这些殖民地过去忍受苦难的经过,也是他们现在不得不改变政府制度的原因。当今大不列颠王国的历史,就是屡屡伤害和掠夺这些殖民地的历史,其直接目标就是要在各州之上建立一个独裁暴政。为了证明上述句句属实,现将事实公诸于世,让公正的世人作出评判。
|
|
||||||
|
|
||||||
他拒绝批准对公众利益最有益、最必需的法律。
|
|
||||||
|
|
||||||
他禁止他的殖民总督批准刻不容缓、极端重要的法律,要不就先行搁置这些法律直至征得他的同意,而这些法律被搁置以后,他又完全置之不理。
|
|
||||||
|
|
||||||
他拒绝批准便利大地区人民的其他的法律,除非这些地区的人民情愿放弃自己在自己在立法机构中的代表权;而代表权对人民是无比珍贵的,只有暴君才畏惧它。
|
|
||||||
|
|
||||||
他把各州的立法委员召集到一个异乎寻常、极不舒适而有远离他们的档案库的地方去开会,其目的无非是使他们疲惫不堪,被迫就范。
|
|
||||||
|
|
||||||
他一再解散各州的众议院,因为后者坚决反对他侵犯人民的权利。
|
|
||||||
|
|
||||||
他在解散众议院之后,又长期拒绝另选他人,于是这项不可剥夺的立法权便归由普通人民来行使,致使在这其间各州仍处于外敌入侵和内部骚乱的种种危险之中。
|
|
||||||
|
|
||||||
他力图阻止各州增加人口,为此目的,他阻挠外国人入籍法的通过,拒绝批准其他鼓励移民的法律,并提高分配新土地的条件。
|
|
||||||
|
|
||||||
他拒绝批准建立司法权利的法律,以阻挠司法的执行。
|
|
||||||
|
|
||||||
他迫使法官为了保住任期、薪金的数额和支付而置于他个人意志的支配之下。
|
|
||||||
|
|
||||||
他滥设新官署,委派大批官员到这里骚扰我们的人民,吞噬他们的财物。
|
|
||||||
|
|
||||||
他在和平时期,未经我们立法机构同意,就在我们中间维持其常备军。
|
|
||||||
|
|
||||||
他施加影响,使军队独立于文官政权之外,并凌驾于文官政权之上。
|
|
||||||
|
|
||||||
他同他人勾结,把我们置于一种既不符合我们的法规也未经我们法律承认的管辖之下,而且还批准他们炮制的各种伪法案,以便任其在我们中间驻扎大批武装部队;不论这些人对我们各州居民犯下何等严重的谋杀罪,他可用加审判来庇护他们,让他们逍遥法外;他可以切断我们同世界各地的贸易;未经我们同意便向我们强行征税;在许多案件中剥夺我们享有陪审制的权益;以莫须有的罪名把我们押送海外受审;他在一个邻省废除了英国法律的自由制度,在那里建立专制政府,扩大其疆域,使其立即成为一个样板和合适的工具,以便向这里各殖民地推行同样的专制统治;他取消我们的许多特许状,废除我们最珍贵的法律并从根本上改变我们各州政府的形式;他终止我们立法机构行使权力,宣称他们自己拥有在任何情况下为我们制定法律的权力。
|
|
||||||
|
|
||||||
他们放弃设在这里的政府,宣称我们已不属他们保护之列,并向我们发动战争。
|
|
||||||
|
|
||||||
他在我们的海域里大肆掠夺,蹂躏我们的沿海地区,烧毁我们的城镇,残害我们人民的生命。
|
|
||||||
|
|
||||||
他此时正在运送大批外国雇佣兵,来从事其制造死亡、荒凉和暴政的勾当,其残忍与卑劣从一开始就连最野蛮的时代也难以相比,他已完全不配当一个文明国家的元首。
|
|
||||||
|
|
||||||
他强迫我们在公海被他们俘虏的同胞拿起武器反对自己的国家,使他们成为残杀自己亲友的刽子手,或使他们死于自己亲友的手下。
|
|
||||||
|
|
||||||
他在我们中间煽动内乱,并竭力挑唆残酷无情的印地安蛮子来对付我们边疆的居民,而众所周知,印地安人作战的准则是不分男女老幼、是非曲直,格杀勿论。
|
|
||||||
|
|
||||||
在遭受这些压迫的每一阶段,我们都曾以最谦卑的言辞吁请予以纠正。而我们一次又一次的情愿,却只是被报以一次又一次的伤害。
|
|
||||||
|
|
||||||
一个君主,其品格被他的每一个只有暴君才干的出的行为所暴露时,就不配君临自由的人民。
|
|
||||||
|
|
||||||
我们并不是没有想到我们英国的弟兄。他们的立法机关想把无理的管辖权扩展到我们这里来,我们时常把这个企图通知他们。我们也曾把我们移民来这里和在这里定居的情况告诉他们。我们曾恳求他们天生的正义感和雅量,念在同种同宗的分上,弃绝这些掠夺行为,因为这些掠夺行为难免会使我们之间的关系和来往中断。可他们对这种正义和同宗的呼声也同样充耳不闻。因此,我们不得不宣布脱离他们,以对待世界上其他民族的态度对待他们:同我交战者,就是敌人;同我和好者,即为朋友。
|
|
||||||
|
|
||||||
因此我们这些在大陆会议上集会的美利坚合众国的代表们,以各殖民地善良人民的名义,并经他们授权,向世界最高裁判者申诉,说明我们的严重意向,同时郑重宣布:
|
|
||||||
|
|
||||||
我们这些联合起来的殖民地现在是,而且按公理也应该是,独立自由的国家;我们对英国王室效忠的全部义务,我们与大不列颠王国之间大不列颠一切政治联系全部断绝,而且必须断绝。
|
|
||||||
|
|
||||||
作为一个独立自由的国家,我们完全有权宣战、缔和、结盟、通商和采取独立国家有权采取的一切行动。
|
|
||||||
|
|
||||||
我们坚定地信赖神明上帝的保佑,同时以我们的生命、财产和神圣的名誉彼此宣誓来支持这一宣言
|
|
||||||
|
|
||||||
## 獨立宣言(傳統中文)
|
|
||||||
|
|
||||||
1776 年 7 月 4 日,美利堅合眾國十三州議會一致通過的宣言。
|
|
||||||
|
|
||||||
在人類事務發展的過程中,當一個民族必須解除同另一個民族的聯繫,並按照自然法則和上帝的旨意,以獨立平等的身份立於世界列國之林時,出於對人類輿論的尊重,必須把驅使他們獨立的原因予以宣佈。
|
|
||||||
|
|
||||||
我們認為下述真理是不言而喻的:人人生而平等,造物主賦予他們若幹不可讓與的權利,其中包括生存權、自由權和追求幸福的權利。為了保障這些權利,人類才在他們中間建立政府,而政府的正當權力,則是經被治者同意所授予的。任何形式的政府一旦對這些目標的實現起破壞作用時,人民便有權予以更換或廢除,以建立一個新的政府。新政府所依據的原則和組織其權力的方式,務使人民認為唯有這樣才最有可能使他們獲得安全和幸福。若真要審慎地來說,成立多年的政府是不應當由於無關緊要的和一時的原因而予以更換的,過去的一切經驗都說明,任何苦難,只要尚能忍受,人類還是情願忍受,也不想為申冤而廢除他們久已習慣了的政府形式。然而,當始終追求同一目標的一系列濫用職權和強取豪奪的行為表明政府企圖把人民置於專制暴政之下時,人民就有權,也有義務,去推翻這樣的政府,並為其未來的安全提供新的保障。這就是這些殖民地過去忍受苦難的經過,也是他們現在不得不改變政府制度的原因。當今大不列顛國王的歷史,就是屢屢傷害和掠奪這些殖民地的歷史,其直接目標就是要在各州之上建立一個獨裁暴政,為了證明上述句句屬實,現將事實公諸於世,讓公正的世人作出評判。
|
|
||||||
|
|
||||||
他拒絕批准對公眾利益最有益、最必需的法律。
|
|
||||||
|
|
||||||
他禁止他的殖民總督批准刻不容緩、極端重要的法律,要不就先行擱置這些法律直至徵得他的同意,而這些法律被擱置以後,他又完全置之不理。
|
|
||||||
|
|
||||||
他拒絕批准便利大地區人民的其他法律,除非這些地區的人民情願放棄自己在立法機構中的代表權,而代表權對人民是無比珍貴的,只有暴君才畏懼它。
|
|
||||||
|
|
||||||
他把各州的立法委員會召集到一個異乎尋常、極不舒適而又遠離它們的檔案庫的地方去開會,其目的無非是使他們疲憊不堪,被迫就範。
|
|
||||||
|
|
||||||
他一再解散各州的眾議院,因為後者堅決反對他侵犯人民的權利。
|
|
||||||
|
|
||||||
他在解散眾議院之後,又長期拒絕另選他人,於是這項不可剝奪的立法權便歸由普通人民來行使,致使在這期間各州仍處於外敵入侵和內部騷亂的種種危險之中。
|
|
||||||
|
|
||||||
他力圖阻止各州增加人口,為此目的,他阻撓外國人入籍法的通過,拒絕批准其他鼓勵移民的法律,並提高分配新土地的條件。
|
|
||||||
|
|
||||||
他拒絕批准建立司法權力的法律,以阻撓司法的執行。
|
|
||||||
|
|
||||||
他迫使法官為了保住任期、薪金的數額和支付而置於他個人意志的支配之下。
|
|
||||||
|
|
||||||
他濫設新官署,委派大批官員到這裏騷擾我們的人民,吞噬他們的財物。
|
|
||||||
|
|
||||||
他在和平時期,未經我們立法機構同意,就在我們中間維持其常備軍。
|
|
||||||
|
|
||||||
他施加影響,使軍隊獨立於文官政權之外,並淩駕於文官政權之上。
|
|
||||||
|
|
||||||
他同他人勾結,把我們置於一種既不符合我們的法規也未經我們法律承認的管轄之下,而且還批准他們炮製的各種偽法案,以便任其在我們中間駐紮大批武裝部隊;不論這些人對我們各州居民犯下何等嚴重的謀殺罪,他可用假審判來庇護他們,讓他們追逐法外;他可以切斷我們同世界各地的貿易;未經我們同意便向我們強行徵稅;在許多案件中剝奪我們享有陪審制的權益;以莫須有的罪名把我們押送海外受審;他在一個鄰省廢除了英國法律的自由制度,在那裏建立專制政府,擴大其疆界,使其立即成為一個樣板和合適的工具,以便向這裏各殖民地推行同樣的專制統治;他取消我們的許多特許狀,廢除我們最珍貴的法律並從根本上改變我們各州政府的形式;他中止我們立法機構行使權力,宣稱他們自己擁有在任何情況下為我們制定法律的權力。
|
|
||||||
|
|
||||||
他們放棄設在這裏的政府,宣佈我們已不屬他們保護之列,並向我們發動戰爭。
|
|
||||||
|
|
||||||
他在我們的海域大肆掠奪,蹂躪我們的沿海地區,燒燬我們的城鎮,殘害我們人民的生命。
|
|
||||||
|
|
||||||
他此時正在運送大批外國僱傭兵,來從事其製造死亡、荒涼和暴政的勾當,其殘忍與卑劣從一開始就連最野蠻的時代也難以相比,他已完全不配當一個文明國家的元首。
|
|
||||||
|
|
||||||
他強迫我們在公海被他們俘虜的同胞拿起武器反對自己的國家,使他們成為殘殺自己親友的劊子手,或使他們死於自己親友的手下。
|
|
||||||
|
|
||||||
他在我們中間煽動內亂,並竭力挑唆殘酷無情的印地安蠻子來對付我們邊疆的居民,而眾所周知,印地安人作戰的準則是不分男女老幼,是非曲直,格殺勿論。
|
|
||||||
|
|
||||||
在遭受這些壓迫的每一階段,我們都曾以最謙卑的言辭籲請予以糾正。而我們一次又一次的請願,卻只是被報以一次又一次的傷害。
|
|
||||||
|
|
||||||
一個君主,其品格被他的每一個只有暴君才幹得出的行為所暴露時,就不配君臨自由的人民。
|
|
||||||
|
|
||||||
我們並不是沒有想到我們英國的弟兄。他們的立法機關想把無理的管轄權擴展到我們這裏來,我們時常把這個企圖通知他們。我們也曾把我們移民來這裏和在這裏定居的情況告訴他們。我們曾懇求他們天生的正義感和雅量,念在同種同宗的份上;棄絕這些掠奪行為,因為這些掠奪行為難免會使我們之間的關係和來往中斷。可他們對這種正義和同宗的呼聲也同樣充耳不聞。因此,我們不得不宣佈脫離他們,以對待世界上其他民族的態度對待他們:同我交戰者,就是敵人;同我和好者,即為朋友。
|
|
||||||
|
|
||||||
因此;我們這些在大陸會議上集會的美利堅合眾國的代表們,以各殖民地善良人民的名義,並經他們授權,向世界最高裁判者申訴,說明我們的嚴正意向,同時鄭重宣佈:我們這些聯合起來的殖民地現在是,而且按公理也應該是,獨立自由的國家;
|
|
||||||
|
|
||||||
我們取消對英國王室效忠的全部義務,我們與大不列顛王國之間的一切政治聯繫從此全部斷絕,而且必須斷絕;作為一個獨立自由的國家,我們完全有權宣戰、締和、結盟、通商和採取獨立國家有權採取的一切行動。我們堅定地信賴神明上帝的保佑,同時以我們的生命、財產和神聖的名譽彼此宣誓來支援這一宣言。
|
|
||||||
|
|
||||||
## 独立宣言(日本語)
|
|
||||||
|
|
||||||
人類の歴史において、ある国民が、他の国民とを結び付けてきた政治的なきずなを断ち切り、世界の諸 国家の間で、自然の法と自然神の法によって与えられる独立平等の地位を占めることが必要となったとき、全世界の人々の意見を真摯に尊重するならば、その国の人々は自分たちが分離せざるを得なくなった理由 について公に明言すべきであろう。
|
|
||||||
|
|
||||||
われわれは、以下の事実を自明のことと信じる。すなわち、すべての人間は生まれながらにして平等で あり、その創造主によって、生命、自由、および幸福の追求を含む不可侵の権利を与えられているという こと。こうした権利を確保するために、人々の間に政府が樹立され、政府は統治される者の合意に基づい て正当な権力を得る。そして、いかなる形態の政府であれ、政府がこれらの目的に反するようになったと きには、人民には政府を改造または廃止し、新たな政府を樹立し、人民の安全と幸福をもたらす可能性が 最も高いと思われる原理をその基盤とし、人民の安全と幸福をもたらす可能性が最も高いと思われる形の 権力を組織する権利を有するということ、である。もちろん、長年にわたり樹立されている政府を軽々し い一時的な理由で改造すべきではないことは思慮分別が示す通りである。従って、あらゆる経験が示すよ うに、人類は、慣れ親しんでいる形態を廃止することによって自らの状況を正すよりも、弊害が耐えられ るものである限りは、耐えようとする傾向がある。しかし、権力の乱用と権利の侵害が、常に同じ目標に 向けて長期にわたって続き、人民を絶対的な専制の下に置こうとする意図が明らかであるときには、その ような政府を捨て去り、自らの将来の安全のために新たな保障の組織を作ることが、人民の権利であり義 務である。これらの植民地が耐え忍んできた苦難は、まさにそうした事態であり、そして今、まさにその ような必要性によって、彼らはこれまでの政府を変えることを迫られているのである。現在の英国王の治世の歴史は、度重なる不正と権利侵害の歴史であり、そのすべてがこれらの諸邦に対する絶対専制の確立 を直接の目的としている。このことを例証するために、以下の事実をあえて公正に判断する世界の人々に 向けて提示することとする。
|
|
||||||
|
|
||||||
国王は、公共の利益にとって最も有益かつ必要である法律の承認を拒否してきた。
|
|
||||||
|
|
||||||
国王は、国王自らの承認が得られるまで執行を保留するとうたわれていない法律の場合は、緊急かつ切 迫した重要性を持つ法律であったとしても、植民地の総督に対し、そのような法律を通過させることを禁 止した。また、保留条項のある法律に関しては、まったく注意を払わず、放置した。
|
|
||||||
|
|
||||||
国王は、人民の英国議会における代表権を放棄しなければ、広大な地域の人民のためとなるその他の法 律を通過させることを拒否すると威嚇した。こうした権利は、人民にとって計り知れないほど貴重なもの であり、それを恐れるのは専制君主のみである。
|
|
||||||
|
|
||||||
国王は、立法府を疲弊させ、国王の政策に忍従させることを唯一の目的として、定例の会場とは違う不 便な場所、また議会の公文書の保管所から離れた場所で議会を召集した。
|
|
||||||
|
|
||||||
国王は、植民地の代議院が国王による人民の権利侵害に対し果敢に断固として反対したという理由で、各代議院を何度も解散させた。
|
|
||||||
|
|
||||||
国王は、そのような解散を行った後、新たに各代議院を選出することを長期にわたって拒否してきた。それにより、消滅させることのできない立法権の行使は、人民全体に戻されるところとなり、その間、諸 邦は外からの侵略および国内の動乱のあらゆる危険にさらされた。
|
|
||||||
|
|
||||||
国王は、諸邦への人口増加を防止しようと努めた。その目的のために外国人帰化法を妨げ、この地への 移住を奨励するその他の法律の通過を拒み、新たな土地取得の条件を厳しくした。
|
|
||||||
|
|
||||||
国王は、司法権を確立する法律を承認することを拒むことによって、司法の執行を妨げてきた。
|
|
||||||
|
|
||||||
国王は、判事の任期およびその給与の額と支払方法を、国王の一存で左右できるようにした。
|
|
||||||
|
|
||||||
国王は、おびただしい数の官職を新たに設け、この植民地の住民を困らせ、その財産を消耗させるため に、多数の役人を派遣してきた。
|
|
||||||
|
|
||||||
国王は、われわれの立法府の同意を得ることなく、平時においてもこの地に常備軍を駐留させている。
|
|
||||||
|
|
||||||
国王は、軍隊を、文民統制から独立させ、かつそれよりも優位にたたせるような措置をとってきた。
|
|
||||||
|
|
||||||
国王は、他者と共謀し、われわれの政体とは相容れない、またわれわれの法律によって認められていな い司法権にわれわれを従わせようとしてきた。そして、見せかけの立法行為による以下のような法律を承 認してきた――
|
|
||||||
|
|
||||||
われわれの間に大規模な軍隊を宿営させる法律。
|
|
||||||
|
|
||||||
その軍隊が諸邦の住民に対して殺人を犯すようなことがあった場合でも、見せかけばかりの裁判によっ て彼らを処罰から免れさせる法律。
|
|
||||||
|
|
||||||
われわれの世界各地との貿易を遮断する法律。
|
|
||||||
|
|
||||||
われわれの同意なしにわれわれに課税をする法律。
|
|
||||||
|
|
||||||
多くの裁判において、陪審による裁判の恩恵を奪う法律。
|
|
||||||
|
|
||||||
われわれを偽りの罪で裁くために海を越えて移送する法律。
|
|
||||||
|
|
||||||
隣接した王領植民地で英国法の自由な制度を廃止し、そこに専制的な政府を樹立し、しかもその境界を 拡張することによって、その政府を、われわれの植民地に同様の専制統治を導入するための先例とし、ま た格好の手段とする法律。
|
|
||||||
|
|
||||||
植民地の設立特許状を剥奪し、われわれの最も貴重な法律を廃止し、われわれの政府の形態を根本的に 変える法律。
|
|
||||||
|
|
||||||
植民地の立法機関を一時停止させ、いかなる事項においてもわれわれに代わって英国議会が立法を行う 権限を与えられていると宣言する法律。
|
|
||||||
|
|
||||||
国王は、われわれを国王による保護の対象外であると宣言し、われわれに対し戦争を仕掛けることに よって、植民地での統治権を放棄した。
|
|
||||||
|
|
||||||
国王は、われわれの領海で略奪行為を行い、沿岸地域を蹂躙し、町を焼き払い、人民の命を奪った。
|
|
||||||
|
|
||||||
国王は、最も野蛮な時代にもほとんど例を見ない、およそ文明国家の長として全くふさわしくない残忍 さと背信行為の数々で、すでに始められている死と荒廃と専制の事業を完遂するために、現に外国人傭兵 の大軍を輸送している。
|
|
||||||
|
|
||||||
国王は、公海で捕虜となったわれわれの同胞に、祖国に対して武器を取らせ、友人・兄弟に対する処刑 人になるよう、あるいは自らの手で自ら命を落とすよう、強要してきた。
|
|
||||||
|
|
||||||
国王は、われわれの間に内乱を引き起こそうと扇動し、また、年齢・性別・身分を問わない無差別の破 壊を戦いの規則とすることで知られる、情け容赦のない野蛮なインディアンを、辺境地帯の住人に対して けしかけようとした。
|
|
||||||
|
|
||||||
こうした弾圧のあらゆる段階で、われわれは最も謙虚な言辞で是正を嘆願してきた。われわれの度重なる 嘆願に対しては、度重なる権利侵害で応えたに過ぎない。このように、専制君主の定義となり得る行為を 特徴とする人格を持つ君主は、自由な人民の統治者として不適任である。
|
|
||||||
|
|
||||||
またわれわれは英国の同胞たちに対しても注意を怠ってきたわけではない。われわれは、彼らの議会が われわれに対してまで不当な権限を押し広げようとする企てについて、折に触れて彼らに注意を促してき た。また、われわれがこの地へ移住し入植した状況を、彼らに改めて思い起こさせてきた。彼らの生来の 遵法精神と寛大さに訴えるとともに、相互の結びつきと親交が必ずや断ち切られることとなるこうした国 王の権利の侵害を認めないよう、われわれの血縁的なきずなをとおして訴えてきた。しかし彼ら英国の同 胞も、正義の声と血縁の訴えに耳を貸そうとしてはいない。従ってわれわれは、分離を宣言する必要性を 認めざるを得ず、彼らに対して、他のすべての人々と同様、戦時においては敵、平和時においては友とみ なさざるを得ない。
|
|
||||||
|
|
||||||
従ってわれわれアメリカ連合諸邦の代表は、大陸会議に参集し、われわれの意図が公正であることを、世界の最高の審判者に対して訴え、これらの植民地の善良な人民の名において、そしてその権威において、以下のことを厳粛に公表し宣言する。すなわち―これらの連合した植民地は自由な独立した国家であり、そうあるべき当然の権利を有する。これらの植民地は英国王に対するあらゆる忠誠の義務から完全に解放 され、これらの植民地と英国との政治的な関係はすべて解消され、また解消されるべきである。そして自 由で独立した国家として、戦争を始め、講和を締結し、同盟を結び、通商を確立し、その他独立国家が当 然の権利として実施できるすべての行為を実施する完全な権限を有する―と。そして、われわれは、この 宣言を支持するために、神の摂理による保護を強く信じ、われわれの生命、財産、および神聖な名誉をか けて相互に誓う。
|
|
||||||
|
|
||||||
## 미국 독립 선언서(한국어)
|
|
||||||
|
|
||||||
인류의 역사에서 한 민족이 다른 한 민족과의 정치적 결합을 해체하고 세계의 여러 나라 사이에서 자연법과 자연의 신의 법이 부여한 독립, 평등의 지위를 차지하는 것이 필요하게 되었을 때, 인류의 신념에 대한 엄정한 고려는 우리로 하여금 독립을 요청하는 여러 원인을 선언하지 않을 수 없게 한다.
|
|
||||||
|
|
||||||
우리들은 다음과 같은 것을 자명한 진리라고 생각한다. 즉, 모든 사람은 평등하게 태어났으며, 조물주는 몇 개의 양도할 수 없는 권리를 부여했으며, 그 권리 중에는 생명과 자유와 행복의 추구가 있다. 이 권리를 확보하기 위하여 인류는 정부를 조직했으며, 이 정부의 정당한 권력은 인민의 동의로부터 유래하고 있는 것이다. 또 어떠한 형태의 정부이든 이러한 목적을 파괴할 때에는 언제든지 정부를 변혁 내지 폐지하여 인민의 안전과 행복을 가장 효과적으로 가져올 수 있는, 그러한 원칙에 기초를 두고 그러한 형태로 기구를 갖춘 새로운 정부를 조직하는 것은 인민의 권리인 것이다. 진실로 인간의 심려는 오랜 역사를 가진 정부를 천박하고도 일시적인 원인으로 변경해서는 안 된다는 것, 인간에게는 악폐를 참을 수 있는 데까지는 참는 경향이 있다는 것을 가르쳐 줄 것이다. 그러나 오랜 동안에 걸친 학대와 착취가 변함 없이 동일한 목적을 추구하고 인민을 절대 전제 정치 밑에 예속시키려는 계획을 분명히 했을 때에는, 이와 같은 정부를 타도하고 미래의 안전을 위해서 새로운 보호자를 마련하는 것은 그들의 권리이며 또한 의무인 것이다. 이와 같은 것이 지금까지 식민지가 견디어 온 고통이었고, 이제야 종래의 정부를 변혁해야 할 필요성이 바로 여기에 있는 것이다. 대영제국의 현재 국왕의 역사는 악행과 착취를 되풀이한 역사이며, 그 목적은 직접 이 땅에 절대 전제 정치를 세우려는 데 있었다. 지금 이러한 사실을 밝히기 위하여 다음의 사실을 공정하게 사리를 판단하는 세계에 표명하는 바이다.
|
|
||||||
|
|
||||||
국왕은 공익을 위해 대단히 유익하고 필요한 법률을 허가하지 않았다.
|
|
||||||
|
|
||||||
국왕은 긴급이 요구되는 중요한 법률이라 할지라도 그가 동의하지 않으면 시행해서는 안 된다고 식민지 총독에게 명령했다. 이렇게 하여 시행이 안 된 법률을 허가할 수 없다고 했다.
|
|
||||||
|
|
||||||
국왕은 우리를 괴롭혀 결국은 그의 정책에 복종시키기 위하여 입법 기관의 양원을 공문서 보관소로부터 멀리 떨어진 유별나고 불편한 장소에 동시에 소집했다.
|
|
||||||
|
|
||||||
국왕은 인민의 권리를 침해한 데 대하여 민의원이 단호하게 반발하면 몇 번이고 민의원을 해산했다.
|
|
||||||
|
|
||||||
국왕은 민의원을 이렇게 해산한 뒤 오랫동안 대의원의 선출을 허가하지 않았다. 그러나 입법권이라는 것은 완전히 폐지할 수는 없으므로, 입법권은 결국 인민 일반에게 돌아와 다시 행사하게 되었지만, 그 동안에 식민지는 내우외환의 온갖 위협에 당면하지 않을 수 없었다.
|
|
||||||
|
|
||||||
국왕은 식민지의 인구를 억제하는 데에도 힘을 썼다. 이를 위하여 외국인의 귀화법에 반대했고, 외국인의 이주를 장려하는 법률도 허가하지 않았으며, 토지를 새로이 취득하는 데에도 여러 가지 조건을 붙여 까다롭게 했다.
|
|
||||||
|
|
||||||
국왕은 사법권을 수립하는 데 관한 법률을 허가하지 않음으로써 사법 행정에도 반대했다.
|
|
||||||
|
|
||||||
국왕은 판사의 임기, 봉급의 액수와 지불에 관해 오로지 국왕의 의사에만 따르도록 했다.
|
|
||||||
|
|
||||||
국왕은 우리들 인민을 괴롭히고 인민의 재산을 축내기 위하여 수많은 새로운 관직을 만들고, 수많은 관리를 식민지에 보냈다.
|
|
||||||
|
|
||||||
국왕은 평화시에도 우리의 입법 기관의 동의 없이 상비군을 주둔시켰다.
|
|
||||||
|
|
||||||
국왕은 다른 기관과 결탁하여 우리의 헌정이 인정하지 않고 우리의 법률이 승인하지 않는 사법권에 예속시키려 했고, 식민지에 대하여 입법권을 주장하는 영국 의회의 여러 법률을 허가했다. 즉,
|
|
||||||
|
|
||||||
대규모의 군대를 우리들 사이에 주둔시키고,
|
|
||||||
|
|
||||||
군대가 우리들 주민을 살해해도 기만적 재판을 해서 이들을 처벌받지 않도록 하고,
|
|
||||||
|
|
||||||
우리와 전세계와의 무역을 차단하고,
|
|
||||||
|
|
||||||
우리의 동의 없이 세금을 부과하고,
|
|
||||||
|
|
||||||
수많은 사건에서 배심 재판을 받는 혜택을 박탈하고,
|
|
||||||
|
|
||||||
허구적인 범죄를 재판하기 위하여 우리를 본국으로 소환하고,
|
|
||||||
|
|
||||||
우리와 인접한 식민지에서 영국의 자유로운 법률 제도를 철폐하고, 전제적 정부를 수립하여 다시 그 영역을 넓혀 이 정부를 모범으로 삼아 이 식민지에도 동일한 절대적 통치를 도입하는 적절한 수단으로 하고, 우리의 특허장을 박탈하고, 우리의 귀중한 법률을 철폐하고, 우리의 정부 형태를 변경하고, 우리의 입법 기관의 기능을 정지시키고, 어떠한 경우든 우리를 대신하여 법률을 제정할 수 있는 권한이 있다고 선언하는, 이러한 법률을 허가한 것이다.
|
|
||||||
|
|
||||||
국왕은 우리를 그의 보호 밖에 둔다고 선언하고, 우리에게 전쟁을 벌임으로써 식민지에 대한 통치를 포기했다.
|
|
||||||
|
|
||||||
국왕은 우리의 바다에서 약탈을 자행하고, 우리의 해안을 습격하고, 우리의 도시를 불사르고, 우리들 주민의 생명을 빼앗았다.
|
|
||||||
|
|
||||||
국왕은 가장 야만적인 시대에도 그 유례가 없고 문명국의 원수로는 도저히 어울리지 않는 잔학과 배신의 상황을 만들고, 이와 더불어 이미 착수한 죽음과 황폐와 포학의 과업을 완수하기 위하여 이 시간에도 외국 용병 대부대를 수송하고 있다.
|
|
||||||
|
|
||||||
국왕은 해상에서 포로가 된 우리들 동포 시민에게 그들이 사는 식민지에 대하여 무기를 들거나, 우리의 벗과 형제 자매의 사형을 집행하거나, 그렇지 않으면 그들의 손에 죽기를 강요했다.
|
|
||||||
|
|
||||||
국왕은 우리들 사이에 내란을 선동했고, 변경의 주민에 대하여는 연령, 남녀, 신분의 여하를 막론하고 무차별로 살해하는 것을 전쟁의 규칙으로 하는, 무자비한 인디언을 자기 편으로 하려고 했다.
|
|
||||||
|
|
||||||
이러한 탄압을 받을 때마다 그때그때 우리는 겸손한 언사로써 시정을 탄원했던 것이다. 그러나 우리의 여러 차례의 진정에 대하여 돌아온 것은 여러 차례의 박해에 지나지 않았다. 이와 같이 그 성격이 모든 행동에 있어서 폭군이라는 정의를 내리지 않을 수 없는 국왕은 자유로운 인민의 통치자로서는 적합하지 않은 것이다.
|
|
||||||
|
|
||||||
우리는 또한 영국의 형제 자매에게도 주의를 환기시키는 데 부족함이 없었다. 우리는 영국 의회가 우리를 억압하려고 부당한 사법권을 넓히려고 하는 데 대하여도 수시로 경고를 했다. 우리는 우리가 아메리카로 이주하여 식민을 하게 된 제반 사정을 다시 한 번 상기시켰다. 우리는 그들의 타고난 정의감과 아량에 대하여도 호소한 바 있었다. 그리고 그들의 피를 같이 나누고 있다는 것에 호소하여 우리와의 연결과 결합을 결국에는 단절시키는 것이 불가피한 이러한 탄압을 거부해 줄 것을 탄원하기도 했다. 그러나 이들 또한 정의와 혈연의 소리에 귀를 기울이지 않았다. 그러므로 우리는 우리가 영국으로부터 독립해야 할 사정을 고발할 필요성을 묵묵히 받아들이면서 세계의 다른 국민에게 대하듯이 영국인에 대하여도 전시에는 적으로, 평화시에는 친구로 대하지 않을 수 없다는 것을 주장하는 바이다.
|
|
||||||
|
|
||||||
이에 아메리카의 연합 제 주의 대표들은 전체 회의에 모여서 우리의 공정한 의도를 세계의 최고 심판에 호소하는 바이며, 이 식민지의 선량한 인민의 이름과 권능으로써 엄숙히 발표하고 선언하는 바이다. 이 연합한 제 식민지는 자유롭고 독립된 국가이며, 또 권리에 의거하고 자유롭고 독립된 국가여야 한다. 이 국가는 영국의 왕권에 대한 모든 충성의 의무를 벗으며, 대영제국과의 모든 정치적 관계는 완전히 해소되고 또 해소되어야 한다. 따라서 이 국가는 자유롭고 독립된 국가로서 전쟁을 개시하고 평화를 체결하고 동맹 관계를 협정하고, 통상 관계를 수립하여 독립 국가가 당연히 해야 할 모든 행동과 사무를 할 수 있는 완전한 권리를 갖고 있는 바이다. 우리들은 이에 우리의 생명과 재산과 신성한 명예를 걸고 신의 가호를 굳게 믿으면서 이 선언을 지지할 것을 서로 굳게 맹세하는 바이다.
|
|
||||||
15
data/posts/2025-09-18-create-this-domain.md
Normal file
15
data/posts/2025-09-18-create-this-domain.md
Normal file
@@ -0,0 +1,15 @@
|
|||||||
|
---
|
||||||
|
title: "创建妙妙(lixiyu)的主页"
|
||||||
|
time: "2025-09-18"
|
||||||
|
tags: ["personal", "homepage", "blog", "lixiyu", "miaomiao"]
|
||||||
|
summary: "给妙妙小朋友创建了一个她自己的主页。"
|
||||||
|
---
|
||||||
|
|
||||||
|
### 从Github查找博客模板
|
||||||
|
|
||||||
|
[tailwind-nextjs-starter-blog](https://github.com/timlrx/tailwind-nextjs-starter-blog)
|
||||||
|
[Azurtelier.com](https://github.com/AmosChenZixuan/Azurtelier.com)
|
||||||
|
[nextjs-lexical-blog](https://github.com/PrinOrange/nextjs-lexical-blog)
|
||||||
|
|
||||||
|
### 模板选择
|
||||||
|
由于宝宝还小,日志内容较少,选了一个最简洁的[nextjs-lexical-blog](https://github.com/PrinOrange/nextjs-lexical-blog)
|
||||||
9
ecosystem.config.js
Normal file
9
ecosystem.config.js
Normal file
@@ -0,0 +1,9 @@
|
|||||||
|
module.exports = {
|
||||||
|
apps: [{
|
||||||
|
name: "lixiyu-net",
|
||||||
|
script: "npm",
|
||||||
|
args: "run start",
|
||||||
|
autorestart: true,
|
||||||
|
watch: false
|
||||||
|
}]
|
||||||
|
}
|
||||||
18192
package-lock.json
generated
Normal file
18192
package-lock.json
generated
Normal file
File diff suppressed because it is too large
Load Diff
10
package.json
10
package.json
@@ -1,15 +1,15 @@
|
|||||||
{
|
{
|
||||||
"name": "nextjs-lexical-blog",
|
"name": "lixiyu-net",
|
||||||
"version": "0.0.0",
|
"version": "0.0.0",
|
||||||
"private": true,
|
"private": true,
|
||||||
"author": {
|
"author": {
|
||||||
"name": "Ethan Zhang",
|
"name": "jimlee",
|
||||||
"email": "terminals@outlook.com",
|
"email": "li@2ha.me",
|
||||||
"url": "https://dreams.plus/"
|
"url": "https://2ha.me"
|
||||||
},
|
},
|
||||||
"bugs": {
|
"bugs": {
|
||||||
"email": "terminals@outlook.com",
|
"email": "terminals@outlook.com",
|
||||||
"url": "https://github.com/PrinOrange/nextjs-lexical-blog/issues"
|
"url": "https://code.2ha.me/lixiyu-net/issues"
|
||||||
},
|
},
|
||||||
"scripts": {
|
"scripts": {
|
||||||
"dev": "next dev",
|
"dev": "next dev",
|
||||||
|
|||||||
@@ -6,7 +6,7 @@ export default function Document() {
|
|||||||
// please change the dir prop value in the following code to rtl
|
// please change the dir prop value in the following code to rtl
|
||||||
// Like <Html dir="rtl" lang="en">
|
// Like <Html dir="rtl" lang="en">
|
||||||
// Otherwise, please do not change
|
// Otherwise, please do not change
|
||||||
<Html dir="ltr" lang="en">
|
<Html dir="ltr" lang="zh">
|
||||||
<Head />
|
<Head />
|
||||||
<body>
|
<body>
|
||||||
<Main />
|
<Main />
|
||||||
|
|||||||
@@ -20,7 +20,7 @@ export default function AboutPage() {
|
|||||||
/>
|
/>
|
||||||
<NavBar />
|
<NavBar />
|
||||||
<ContentContainer>
|
<ContentContainer>
|
||||||
<PageTitle>{"ABOUT ME"}</PageTitle>
|
<PageTitle>{"关于妙妙"}</PageTitle>
|
||||||
<Separator />
|
<Separator />
|
||||||
<Introduction />
|
<Introduction />
|
||||||
<Separator />
|
<Separator />
|
||||||
|
|||||||
@@ -14,7 +14,7 @@ export default function FriendsPage() {
|
|||||||
<SEO description={"My Friend Links"} title={`${Config.SiteTitle} - Friends`} />
|
<SEO description={"My Friend Links"} title={`${Config.SiteTitle} - Friends`} />
|
||||||
<NavBar />
|
<NavBar />
|
||||||
<ContentContainer>
|
<ContentContainer>
|
||||||
<PageTitle>{"FRIENDS"}</PageTitle>
|
<PageTitle>{"朋友们"}</PageTitle>
|
||||||
<Separator />
|
<Separator />
|
||||||
<FriendLinkList friends={FriendsList} />
|
<FriendLinkList friends={FriendsList} />
|
||||||
</ContentContainer>
|
</ContentContainer>
|
||||||
|
|||||||
@@ -32,7 +32,7 @@ export default function Home(props: HomePageProps) {
|
|||||||
<NavBar />
|
<NavBar />
|
||||||
<ContentContainer>
|
<ContentContainer>
|
||||||
<HomeCover />
|
<HomeCover />
|
||||||
{props.pinnedPostList.length !== 0 && (
|
{/* {props.pinnedPostList.length !== 0 && (
|
||||||
<div>
|
<div>
|
||||||
<Separator />
|
<Separator />
|
||||||
<h2 className={"caption-font my-5 flex justify-center font-bold text-2xl"}>
|
<h2 className={"caption-font my-5 flex justify-center font-bold text-2xl"}>
|
||||||
@@ -61,7 +61,7 @@ export default function Home(props: HomePageProps) {
|
|||||||
</Button>
|
</Button>
|
||||||
</div>
|
</div>
|
||||||
</div>
|
</div>
|
||||||
)}
|
)} */}
|
||||||
</ContentContainer>
|
</ContentContainer>
|
||||||
<Footer />
|
<Footer />
|
||||||
</Page>
|
</Page>
|
||||||
|
|||||||
Binary file not shown.
|
Before Width: | Height: | Size: 14 KiB After Width: | Height: | Size: 120 KiB |
Binary file not shown.
|
Before Width: | Height: | Size: 456 KiB After Width: | Height: | Size: 594 KiB |
Reference in New Issue
Block a user