upgrade the project
This commit is contained in:
191
data/posts/2023-12-18-The-Master-Theroy-For-Time-Complexity.md
Normal file
191
data/posts/2023-12-18-The-Master-Theroy-For-Time-Complexity.md
Normal file
@@ -0,0 +1,191 @@
|
||||
---
|
||||
title: "The Master Theorem For Time Complexity"
|
||||
subtitle: ""
|
||||
summary: "In this article, we will model the time complexity of divide and conquer using mathematical methods, analyze its asymptotic properties, and provide three methods of calculation."
|
||||
coverURL: ""
|
||||
time: "2023-12-18"
|
||||
tags: ["algorithm", "mathematics", "computation"]
|
||||
noPrompt: false
|
||||
pin: false
|
||||
allowShare: true
|
||||
---
|
||||
|
||||
When we navigate through the ocean of divide and conquer, there's a question that must be addressed—how is the time complexity of divide and conquer algorithms calculated?
|
||||
|
||||
## From Divide and Conquer to Recurrence Relation
|
||||
|
||||
Divide and conquer involves breaking down a large problem into smaller subproblems and then merging the solutions of these subproblems to obtain the solution to the original problem. Recurrence relation is a mathematical way of modeling the time cost of this process.
|
||||
|
||||
Starting with a concrete example makes it easier to understand. Taking merge sort as an example, let $T(n)$ represent the time complexity of the original problem, where $n$ is the size of the input data. In the first split, the original data is divided into two equal parts, each of size $n/2$. Then, recursive calls to merge sort are made on these two parts, and the time complexity of this part is $2 T(n/2)$. Finally, the two sorted subarrays are merged, requiring a time complexity of $\Theta(n)$.
|
||||
|
||||
Based on the analysis above, we can write the recurrence relation for merge sort as follows:
|
||||
|
||||
$$
|
||||
\begin{equation} T(n) = \left\{ \begin{aligned} &\Theta(1) & \text{if } n=1\\ &2 T(n/2) + \Theta(n) & \text{if } n>1 \end{aligned} \right. \tag{1} \end{equation}
|
||||
$$
|
||||
|
||||
It can be imagined that for any divide and conquer algorithm, its time complexity can be expressed as a recurrence relation. The right-hand side of the recurrence relation usually consists of two parts: the total cost of the divided subproblems and the total cost of dividing and merging subproblems. The first part remains a function of $T$, while the second part represents the actual asymptotic complexity.
|
||||
|
||||
Having a recurrence relation is not sufficient to determine the exact time complexity of the algorithm. We need to further calculate the actual solution $T(n)$.
|
||||
|
||||
## Substitution Method
|
||||
|
||||
The first method for solving recurrence relations is called the substitution method. We need to guess the form of the solution first and then use mathematical induction to prove that the guess is correct.
|
||||
|
||||
For Equation (1), let's assume that our guess for the solution is $T(n) = O(n \log n)$. If we remove the asymptotic notation, this equation is equivalent to $T(n) \le c_1 n \log n$, where $c_1$ is any positive constant.
|
||||
|
||||
According to mathematical induction, we first need to establish that the guess holds for small values of $n$. When $n=1$, according to Equation (1), $T(1) = \Theta(1) = d_1$, where $d_1$ is some constant greater than 0. According to the guess, we hope $T(1) \le c_1 \log 1 = 0$, but no matter how we choose $c_1$, this equation cannot hold because $T(1) = d_1$ is always greater than 0. The mathematical induction fails before it even starts.
|
||||
|
||||
However, there is no need to worry; this is just a special case caused by $ \log 1 = 0$. We can place the initial state of mathematical induction at $n>1$ without affecting the results of mathematical induction. We are only interested in the asymptotic properties of $T(n)$ when $n$ is sufficiently large, not in the initial stage.
|
||||
|
||||
Now, let $n = 2$, then $T(2) = 2T(1) + d_2 = 2d_1 + d_2$. We hope that $T(2) \le c_1 \log 2$ holds. Simplifying, we get $c_1 \ge d_1 + d_2/2$. Since $d_1$ and $d_2$ are constants, such $c_1$ exists, and the initial condition holds.
|
||||
|
||||
Next, mathematical induction assumes that the solution holds at $n/2$, i.e., $T(n/2) \le c_1 \frac{n}{2} \log\frac{n}{2} = \frac{1}{2}c_1n(\log n - 1)$. Then we prove that $T(n) \le c_1 n \log n$ also holds.
|
||||
|
||||
Substituting $T(n/2)$ into Equation (1), we get
|
||||
|
||||
$$
|
||||
\begin{equation} \begin{aligned} T(n) & = 2 T\left(\frac{n}{2}\right) + \Theta(n) \\ & \le 2 \frac{1}{2}c_1n(\log n - 1) + d_2n \\ & = c_1 n \log n + (d_2 - c_1) n \\ & \le c_1 n \log n \end{aligned} \end{equation}
|
||||
$$
|
||||
|
||||
Where the last line's inequality requires $d_2 - c_1 < 0$, obviously such $c_1$ exists, so the proof is complete.
|
||||
|
||||
Thus, we have proved that $T(n) = O(n \log n)$ is the solution to the recurrence relation (1). However, this is not the end; this asymptotic notation is not a tight bound. Can we further guess that $T(n) = \Theta(n \log n)$ holds? This is indeed a good idea. So, as we proceed, as long as we can prove that $T(n) = \Omega(n \log n)$ holds, we can obtain the tight bound mentioned above. Removing the asymptotic notation, this equation is equivalent to $T(n) \ge c_2 n \log n$. Using mathematical induction again, confirming that this holds in the initial stage, and then assuming that the solution holds at $n/2$, we can derive that the solution holds at $n$. Therefore, the proof is complete. Since the proof steps are almost identical to those just mentioned, we will not elaborate on them, and you can try it yourself.
|
||||
|
||||
The substitution method relies on accurate guesses, which can be impractical. Therefore, in practice, a more common approach is to find a guess using other methods and then use the substitution method to verify the guess. The recursive tree method we will introduce next provides this possibility.
|
||||
|
||||
## Recursive Tree
|
||||
|
||||
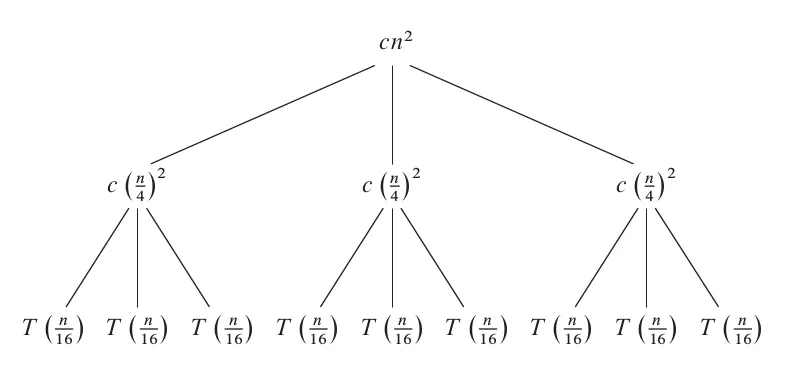
Expanding the recurrence relation layer by layer directly yields a tree structure. For example, let's take $T(n) = 3 T(n/4) + \Theta(n^2)$ as an example and see how to draw its recursive tree.
|
||||
|
||||
Expanding the first layer, we draw three child nodes under the root node.
|
||||
|
||||
Here, $cn^2$ represents the cost of decomposition and merging at this layer, which corresponds to the part represented by $\Theta(n^2)$ in the recurrence relation.
|
||||
|
||||
Next, further expand to the second layer.
|
||||
|
||||
|
||||
|
||||
Here, the cost of each node in the first layer is still $c(\frac{n}{4})^2$, still corresponding to the part represented by $\Theta(n^2)$ in the recurrence relation, but the data size has changed from $n$ to $n/4$.
|
||||
|
||||
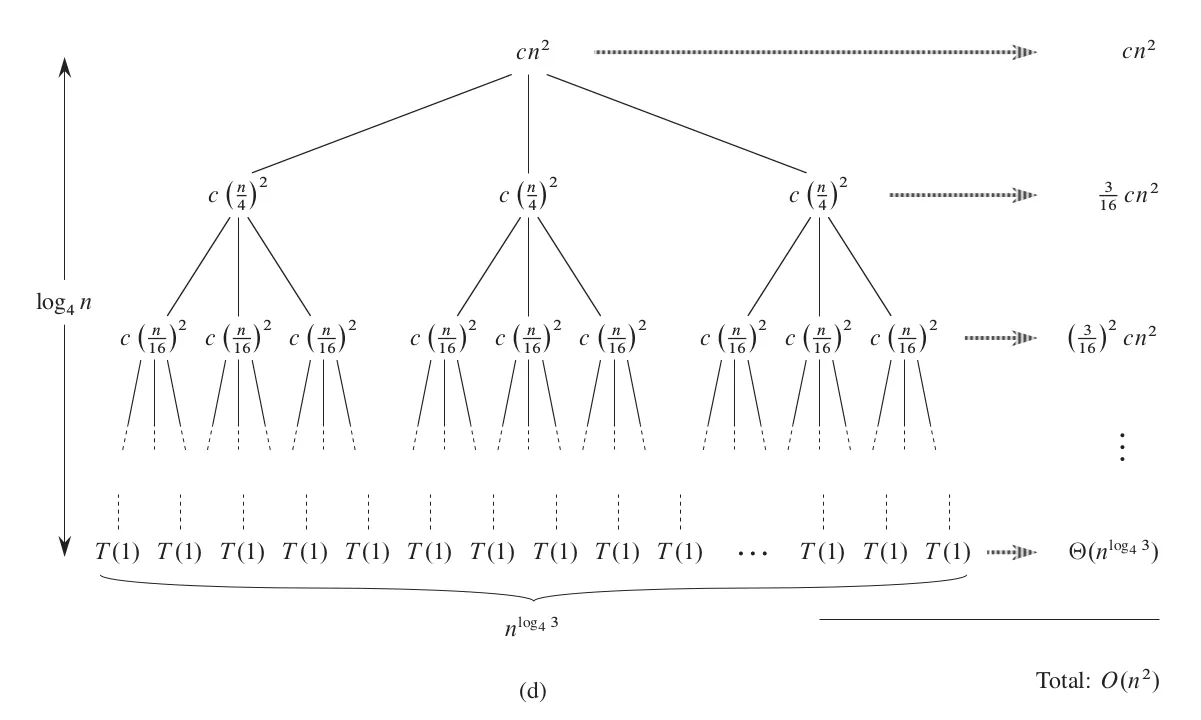
Continue expanding in this way until the leaf nodes.
|
||||
|
||||
|
||||
|
||||
This completes a complete recursive tree. The data size of each layer is reduced to one-fourth of the previous one, until the data size of the leaf node is 1, so the total number of layers is $\log_4 n$. The rightmost side of the figure calculates the total cost of all nodes in each layer, and the calculation is simple: multiply the cost of a single node by the number of nodes in that layer. In the last layer, the cost of a single node is a constant, and the number of nodes is $3^{\log_4 n} = n^{\log_4 3}$, and we denote the total cost as $\Theta(n^{\log_4 3})$.
|
||||
|
||||
Next, we just need to add up the costs of all nodes to obtain the solution to the recurrence relation.
|
||||
|
||||
$$
|
||||
\begin{aligned} T(n) &= cn^2 + \frac{3}{16} cn^2 + \left(\frac{3}{16}\right)^2 cn^2 + \cdots + \left( \frac{3}{16} \right)^{\log_4 n-1} cn^2 + \Theta(n^{\log_4 3}) \\ &=\sum_{i=0}^{\log_4 n-1}{\left(\frac{3}{16}\right)^i cn^2} + \Theta(n^{\log_4 3})\\ &\lt \sum_{i=0}^{\infty}{\left(\frac{3}{16}\right)^i cn^2} + \Theta(n^{\log_4 3}) \\ &= \frac{1}{1 - 3/16}cn^2 + \Theta(n^{\log_4 3}) \\ &= \frac{16}{13} cn^2 + \Theta(n^{\log_4 3}) \\ &= O(n^2) \end{aligned}
|
||||
$$
|
||||
|
||||
Here, in the third line, we made a simplification by replacing a finite geometric series with an infinite geometric series. Although the total size has increased, this infinite decreasing geometric series has a limit, so this replacement can simplify the derivation process. The second term in the fifth line is a lower-order term relative to the first term, so it is discarded, resulting in the final result.
|
||||
|
||||
Similar to before, we have only proven the upper bound of the recurrence relation. Naturally, we want to try whether it can also be proven as a lower bound. In the above equation, each term in the summation contains $cn^2$, and each term is positive, so $T(n) = \Omega(n^2)$ obviously holds. Therefore, the solution to the recurrence relation is $T(n) = \Theta(n^2)$.
|
||||
|
||||
In this example, we directly calculated the solution to the recurrence relation using the recursive tree method. Of course, we can use the substitution method to verify whether this solution is correct. In some cases, it may be slightly difficult to calculate the exact solution using the recursive tree method, but it does not prevent us from making a reasonable guess and then further verifying this guess using the substitution method.
|
||||
|
||||
## Master Theorem
|
||||
|
||||
Both the substitution method and the recursion tree method have their drawbacks. The former requires an accurate guess, while the latter involves drawing a recursion tree and deriving results. If you derive too much, you may find that the forms of most recursive solutions seem to be the same. From the derivation process above, it can be observed that the final solution depends entirely on the sum of costs in the middle layers and has nothing to do with the leaf layer because the latter is a lower-order term. In other recursion trees, the final solution may depend entirely on the cost of the leaf layer, unrelated to the middle layers. Therefore, we may be able to classify recursive formulas and directly write out the final solution according to some rules. This is the idea behind the master theorem.
|
||||
|
||||
When the divide-and-conquer method evenly splits the data each time, the recursive formula generally has the following form.
|
||||
|
||||
$$
|
||||
T(n) = aT\left(\frac{n}{b}\right) + f(n) \tag{2}
|
||||
$$
|
||||
|
||||
where $a$ is a positive integer representing the number of subproblems when dividing each time, $b$ is an integer greater than 1 representing the reduction factor in problem size each time, and $f(n)$ is an asymptotically positive function representing the cost of dividing and merging.
|
||||
|
||||
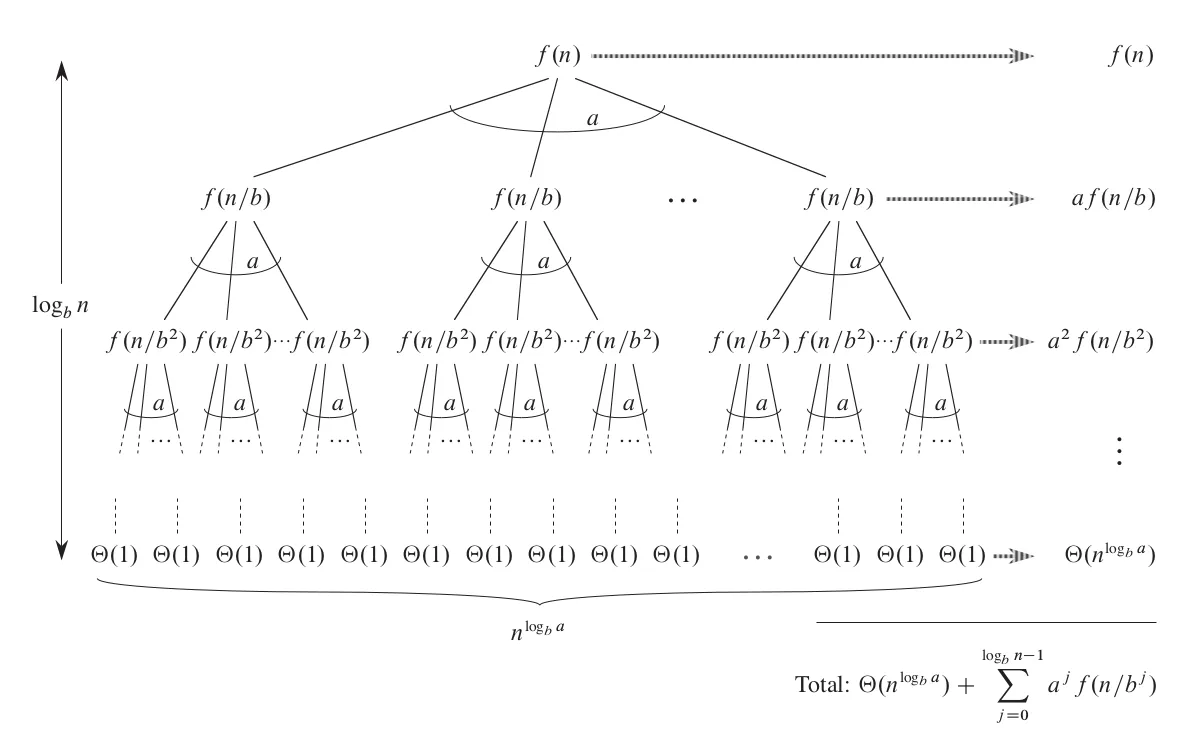
To find a unified solution applicable to any $a$, $b$, and $f(n)$, we still need to use the recursion tree to calculate the costs of all intermediate and leaf nodes and try to derive a simple result.
|
||||
|
||||
|
||||
|
||||
From the graph, we can see that the total cost of all nodes is $T(n) = \Theta(n^{\log_b a}) + \sum_{j=0}^{\log_b n-1}{a^j f(n/b^j)}$. Further derivation requires a breakthrough idea, and I don't know how the original researchers discovered the following pattern, but it is indeed magical.
|
||||
|
||||
Researchers found that the relationship between $f(n)$ and $\Theta(n^{\log_b a})$ determines the final simplified form of $\sum_{j=0}^{\log_b n-1}{a^j f(n/b^j)}$. Define
|
||||
|
||||
$$
|
||||
g(n) = \sum_{j=0}^{\log_b n-1}{a^j f(n/b^j)} \tag{3}
|
||||
$$
|
||||
|
||||
Now let's analyze three cases.
|
||||
|
||||
1. If $\Theta(n^{\log_b a})$ is larger, we can assume that there exists a constant $\epsilon > 0$ such that $f(n) = O(n^{\log_b a-\epsilon})$. Substituting this into the summation formula, it can be simplified to $g(n) = O(n^{\log_b a})$.
|
||||
|
||||
2. If both are equally large, directly substitute into equation (3) and simplify to get $g(n) = \Theta(n^{\log_b a} \log n)$.
|
||||
|
||||
3. If $f(n)$ is larger and, for some constant $c < 1$, for all sufficiently large $n$, $a f(n/b) \le c f(n)$ holds, then it can be deduced that $g(n) = \Theta(f(n))$.
|
||||
|
||||
Here, the complete proof process is not provided, partly because I don't want to make it too long, and secondly, I feel that these proofs are somewhat cumbersome and not very meaningful. Interested students can refer to the original book.
|
||||
|
||||
Substituting the functions $g(n)$ for these three cases into the complete solution, we get:
|
||||
|
||||
- For case 1: $T(n) = \Theta(n^{\log_b a}) + O(n^{\log_b a}) = \Theta(n^{\log_b a})$
|
||||
|
||||
- For case 2: $T(n) = \Theta(n^{\log_b a}) + \Theta(n^{\log_b a} \log n) = \Theta(n^{\log_b a} \log n)$
|
||||
|
||||
- For case 3: $T(n) = \Theta(n^{\log_b a}) + \Theta(f(n)) = \Theta(f(n))$
|
||||
|
||||
Now, for any recursive formula, we only need to determine which case it belongs to and directly substitute into the corresponding formula. To facilitate understanding, let's go through a few examples.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
$T(n) = 9 T(n/3) + n$
|
||||
|
||||
For this recursive formula, we have $a = 9$, $b = 3$, $f(n) = n$. Since $f(n) = n$ is asymptotically smaller than $\Theta(n^2)$, it can be applied to the first case of the master theorem, and the solution is $T(n) = \Theta(n^2)$.
|
||||
|
||||
**Example 2:**
|
||||
|
||||
$T(n) = T(2n/3) + 1$
|
||||
|
||||
For this formula, $a = 1$, $b = 3/2$, $f(n) = 1$. Since $n^{\log_b a} = n^{\log_{3/2} 1} = n^0 = 1$, which is exactly equal to $f(n)$, it can be applied to the second case of the master theorem, and the solution is $T(n) = \Theta(\log n)$.
|
||||
|
||||
**Example 3:**
|
||||
|
||||
$T(n) = 3T(n/4) + n\log n$
|
||||
|
||||
For this formula, $a = 3$, $b = 4$, $f(n) = n\log n$. Since $n^{\log_b a} = n^{\log_4 3} = n^{0.793}$, and $f(n) = n\log n$ is asymptotically larger than $n^{0.793}$, it should consider the third case of the master theorem. However, we need to check if the additional condition holds: for some constant $c < 1$ and all sufficiently large $n$, $a f(n/b) \le c f(n)$ holds. Substituting $a$, $b$, and $f(n)$ into the inequality, we get
|
||||
|
||||
$$
|
||||
3\frac{n}{4}\log\frac{n}{4} \le cn\log n \implies \frac{3}{4}( \log n - 2) \le c\log n \implies \left(\frac{3}{4} - c\right) \log n \le \frac{3}{2}
|
||||
$$
|
||||
|
||||
When $c \ge \frac{3}{4}$, this inequality always holds, and the additional condition is satisfied. Therefore, it can be applied to the third case of the master theorem, and the solution is $T(n) = \Theta(n\log n)$.
|
||||
|
||||
**Example 4:**
|
||||
|
||||
$T(n) = 2T(n/2) + n\log n$
|
||||
|
||||
For this formula, $a = 2$, $b = 2$, $f(n) = n\log n$. Since $n^{\log_b a} = n^{\log_2 2} = n$, and $f(n) = n\log n$ is asymptotically larger than $n$, it should consider the third case of the master theorem. Substituting $a$, $b$, and $f(n)$ into the inequality, we get
|
||||
|
||||
$$
|
||||
2\frac{n}{2}\log\frac{n}{2} \le cn\log n \implies \log n - 1 \le c\log n \implies (1-c)\log n \le 1
|
||||
$$
|
||||
|
||||
When $c \ge 1$, this inequality always holds. However, the additional condition requires $c < 1$, so this case cannot be applied to the third case of the master theorem. In other words, not all recursive formulas of the form $T(n) = a T(n/b) + f(n)$ can be solved using the master theorem; there is a gap between cases two and three. In such cases, we can only use the recursion tree method. Students can try it, and the result will be $T(n) = \Theta(n \log^2 n)$.
|
||||
|
||||
After going through these four examples, have you mastered the master theorem? If you have any questions, please leave a comment, and I will reply as soon as possible.
|
||||
|
||||
The study of algorithms is endless, and the calculation of time complexity is fundamental and should not be underestimated.
|
||||
|
||||
## Details
|
||||
|
||||
Careful readers may notice that in the fourth case mentioned above, although $nlgn$ grows asymptotically faster than $n$, it is not asymptotically greater in the polynomial sense because there is no $\epsilon > 0$ such that $nlgn = \Omega \left( n^{1+\epsilon} \right)$ holds. On the contrary, $nlgn = o \left( n^{1+\epsilon} \right)$ holds for any $\epsilon > 0$. So, in fact, this case does not need to be judged for regular conditions to draw conclusions in advance. However, in the third case in the previous text, I did not emphasize asymptotic greater in the polynomial sense, not because I forgot to write it, but because this condition is not needed at all.
|
||||
|
||||
For any recurrence relation that fits the master theorem format, if it satisfies the regular conditions in case three, then it must satisfy $f\left(n\right) = \Omega \left( n^{log_b a + \epsilon} \right)$." The specific proof details can be found in [this answer](https://cs.stackexchange.com/a/121749/128497) on StackExchange, and are not detailed here.
|
||||
|
||||
Although regular conditions can imply $f\left(n\right) = \Omega \left( n^{log_b a + \epsilon} \right)$, the reverse is not true. We can construct the following function:
|
||||
|
||||
$T\left(n\right) = T\left(n/2\right) + n\left( 2 - \cos n \right)$
|
||||
|
||||
Here, $a=1$, $b=2$, and $f\left(n\right) = n \left( 2 - \cos n \right) = \Omega \left( n^{log_2 1+ \epsilon} \right) = \Omega \left( n^\epsilon \right)$ holds for any $\epsilon \le1$. However, when applying the regular condition:
|
||||
|
||||
$\begin{aligned} f\left(n / 2\right) &\le c f\left(n\right) \\ \frac{n}{2} \left(2 - \cos \frac{n}{2} \right) & \le c \left( 2 - \cos n \right) \end{aligned}$
|
||||
|
||||
For any $c \lt 1$, the right side must be $c \left( 2 - \cos n \right) \lt 3$. However, the left side, when $n$ is large enough, must be greater than $3$. Therefore, this equation cannot hold, and the regular condition is not satisfied.
|
||||
|
||||
## Reference
|
||||
|
||||
These cases are from the Wikipedia entry on [Master theorem](<https://en.wikipedia.org/w/index.php?title=Master_theorem_(analysis_of_algorithms)§ion=7#Inadmissible_equations>).
|
||||
@@ -1,6 +1,6 @@
|
||||
---
|
||||
title: "everything you ever wanted to know about the computer vision"
|
||||
summary: ""
|
||||
summary: "One of the most powerful and compelling types of AI is computer vision which you’ve almost surely experienced in any number of ways without even knowing. Here’s a look at what it is, how it works, and why it’s so awesome (and is only going to get better)."
|
||||
coverURL: "https://miro.medium.com/v2/resize:fit:788/1*8gmgaAkFdI-9OHY5cA93xQ.png"
|
||||
time: "2023-12-25"
|
||||
tags: ["computer-vision"]
|
||||
|
||||
@@ -0,0 +1,704 @@
|
||||
---
|
||||
title: "Taylor formula, taylor theorem, taylor series, taylor expansion"
|
||||
subtitle: ""
|
||||
summary: "This article mainly introduces the content and connection between the four concepts of Taylor's formula, Taylor's theorem, Taylor series and Taylor's expansion."
|
||||
coverURL: ""
|
||||
time: "2024-03-06"
|
||||
tags: ["mathematics"]
|
||||
noPrompt: false
|
||||
pin: false
|
||||
allowShare: true
|
||||
---
|
||||
|
||||
## Taylor Formula
|
||||
|
||||
If the function $f(x)$ is differentiable at point $x_{0}$, i.e.,
|
||||
|
||||
$$
|
||||
\lim_{x \rightarrow x_{0}}{\frac{f(x)-f(x_{0})}{x-x_{0}}}=f'(x_{0})
|
||||
$$
|
||||
|
||||
which is also expressed as
|
||||
|
||||
$$
|
||||
\lim_{x \rightarrow x_{0}}{\frac{f(x)-f(x_{0})}{x-x_{0}}}-f'(x_{0})=0
|
||||
$$
|
||||
|
||||
Rearranging gives
|
||||
|
||||
$$
|
||||
\lim_{x \rightarrow x_{0}}{\frac{f(x)-f(x_{0})-f'(x_{0})(x-x_{0})}{x-x_{0}}}=0
|
||||
$$
|
||||
|
||||
Thus,
|
||||
|
||||
$$
|
||||
f(x)-f(x_{0})-f'(x_{0})(x-x_{0})=o(x-x_{0})(x\rightarrow x_{0})
|
||||
$$
|
||||
|
||||
Rearranging terms yields
|
||||
|
||||
$$
|
||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})(x\rightarrow x_{0})
|
||||
$$
|
||||
|
||||
This implies that near the point $x*{0}$, we can approximate the function $f(x)$ with a first-degree polynomial $f(x*{0})+f'(x*{0})(x-x*{0})$, with an error of $(x-x*{0})$ as a higher-order infinitesimal. Sometimes, such an approximation may be crude, indicating a relatively large error. Thus, naturally, we wonder if we can approximate $f(x)$ using a higher-degree $n$ polynomial to make the error $o((x-x*{0})^{n})$.
|
||||
|
||||
For a polynomial function
|
||||
|
||||
$$
|
||||
f_{n}(x)=a_{0}+a_{1}(x-x_{0})+a_{2}((x-x_{0})^{2})+...+a_{n}((x-x_{0})^{n})
|
||||
$$
|
||||
|
||||
By successively taking its derivatives at $x_{0}$, we obtain
|
||||
|
||||
$$
|
||||
f_{n}(x_{0})=a_{0} \\
|
||||
f_{n}'(x_{0})=a_{1} \\
|
||||
f_{n}''(x_{0})=2!a_{2} \\
|
||||
... \\
|
||||
f_{n}^{(n)}(x_{0})=n!a_{n}
|
||||
$$
|
||||
|
||||
Therefore,
|
||||
|
||||
$$
|
||||
a_{0}=f_{n}(x_{0}) \\
|
||||
a_{1}=\frac{f_{n}'(x_{0})}{1!} \\
|
||||
a_{2}=\frac{f_{n}''(x_{0})}{2!} \\
|
||||
a_{n}=\frac{f_{n}^{(n)}(x_{0})}{n!}
|
||||
$$
|
||||
|
||||
Thus, the coefficients of the polynomial function $f*{n}(x)$ are uniquely determined by its derivatives at point $x*{0}$. This insight inspires us that for a general function $f(x)$, if $f(x)$ has derivatives up to $n$th order at point $x_{0}$, then these derivatives uniquely determine an $n$th degree polynomial
|
||||
|
||||
$$
|
||||
T_{n}(x)=f(x_{0})+\frac{f'(x_{0})}{1!}(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2} \\ +...+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}
|
||||
$$
|
||||
|
||||
This polynomial is called the **Taylor polynomial** of function $f(x)$ at point $x*{0}$, and the coefficients of $T*{n}(x)$
|
||||
|
||||
$$
|
||||
\frac{f^{(k)}(x_{0})}{k!}(k=1,2,...,n)
|
||||
$$
|
||||
|
||||
are termed as **Taylor coefficients**.
|
||||
|
||||
It is evident that the function $f(x)$ and its Taylor polynomial $T*{n}(x)$ have the same function values and derivatives up to the $n$th order at point $x*{0}$, i.e.,
|
||||
|
||||
$$
|
||||
f^{(k)}(x_{0})=T_{n}^{(k)}(x_{0}),\ k=0,1,2,...,n.
|
||||
$$
|
||||
|
||||
Returning to our conjecture, can we prove $f(x)=T*{n}(x)+o((x-x*{0})^{n})$? If this holds, then when approximating function $f(x)$ with the Taylor polynomial $T*{n}(x)$, the error will be as desired, i.e., an error term higher order than $(x-x*{0})^{n}$.
|
||||
|
||||
**Theorem:** If the function $f(x)$ has derivatives up to $n$th order at point $x_{0}$, then
|
||||
|
||||
$$
|
||||
f(x)=T_{n}(x)+ o((x-x_{0})^{n})
|
||||
$$
|
||||
|
||||
i.e.,
|
||||
|
||||
$$
|
||||
f(x)=f(x_{0})+\frac{f'(x_{0})}{1!}(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2} +\\...+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+o((x-x_{0})^{n})
|
||||
$$
|
||||
|
||||
**Proof:** Let
|
||||
|
||||
$$
|
||||
R_{n}(x)=f(x)-T_{n}(x)\\
|
||||
Q_{n}(x)=(x-x_{0})^{n}
|
||||
$$
|
||||
|
||||
It is to be proven that
|
||||
|
||||
$$
|
||||
\lim_{x \rightarrow x_{0}}{\frac{R_{n}(x)}{Q_{n}(x)}}=0
|
||||
$$
|
||||
|
||||
Since
|
||||
|
||||
$$
|
||||
f^{(k)}(x_{0})=T_{n}^{(k)}(x_{0}),\ k=0,1,2,...,n.
|
||||
$$
|
||||
|
||||
Thus,
|
||||
|
||||
$$
|
||||
R_{n}(x_{0})=R'_{n}(x_{0})=...=R^{(n)}_{n}(x_{0})=0
|
||||
$$
|
||||
|
||||
and
|
||||
|
||||
$$
|
||||
Q_{n}(x_{0})=Q'_{n}(x_{0})=...=Q^{(n-1)}_{n}(x_{0})=0 \\ Q^{(n)}_{n}(x_{0})=n!
|
||||
$$
|
||||
|
||||
Because $f^{(n)}(x*{0})$ exists, \
|
||||
Therefore, in a neighborhood $U(x*{0})$ of $x*{0}$, $f(x)$ has a $(n-1)$th order derivative $f^{(n-1)}(x)$. \
|
||||
Thus, when $x\in U^{o}(x*{0})$ and $x\rightarrow x_{0}$, by repeatedly applying L'Hôpital's rule $n-1$ times, we have
|
||||
|
||||
$$
|
||||
\lim_{x \rightarrow x_{0}}{\frac{R_{n}(x)}{Q_{n}(x)}}\\=\lim_{x \rightarrow x_{0}}{\frac{R'_{n}(x)}{Q'_{n}(x)}}\\=...\\=\lim_{x \rightarrow x_{0}}{\frac{R^{(n-1)}_{n}(x)}{Q^{(n-1)}_{n}(x)}}\\=\lim_{x \rightarrow x_{0}}{\frac{f^{(n-1)}(x)-f^{(n-1)}(x_{0})-f^{(n)}(x_{0})(x-x_{0})}{n(n-1)\cdot \cdot \cdot2(x-x_{0})}}\\=\frac{1}{n!}\lim_{x \rightarrow x_{0}}{\left[ \frac{f^{(n-1)}(x)-f^{(n-1)}(x_{0})}{x-x_{0}}-f^{(n)}(x_{0}) \right]}=0
|
||||
$$
|
||||
|
||||
The expression proved by this theorem is termed as the **Taylor formula** for function $f(x)$ at $x_{0}$. Since its corresponding remainder term
|
||||
|
||||
$$
|
||||
R_{n}(x)=f(x)-T_{n}(x)=o((x-x_{0})^{n})
|
||||
$$
|
||||
|
||||
it is also called the **Taylor formula with Peano remainder**. Hence, this expression is also referred to as the **Taylor formula with Peano remainder**.
|
||||
|
||||
**Note:** The Taylor formula (with Peano remainder) is a qualitative expression. Although this expression holds for the entire domain of $f(x)$, its remainder term is meaningful only near the point $x_{0}$. Thus, this expression has strong limitations.
|
||||
|
||||
## Taylor's Theorem
|
||||
|
||||
In order to overcome the drawback of the Taylor formula above, which only allows for a qualitative analysis of functions, we need a more precise quantitative expression to characterize the function $f(x)$. A quantitative expression can more accurately delineate the range of errors when approximating the function $f(x)$ with a polynomial function.
|
||||
|
||||
**Theorem (Taylor's Theorem):** If the function $f(x)$ has continuous derivatives up to $n$th order on $[a, b]$ and has $(n+1)$ st order derivatives on $(a, b)$, then for any given $x, x_{0} \in [a, b]$, there exists at least one point $\xi \in (a, b)$ such that
|
||||
|
||||
$$
|
||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+\dots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}
|
||||
$$
|
||||
|
||||
**Analysis:** From the conditions of the theorem, we can see that the functions $f(x)$ and $(x-x_{0})^{n+1}$ can be "arbitrarily" used on $[a, b]$ using the Mean Value Theorem, hence the proof approach utilizes the Mean Value Theorem.
|
||||
|
||||
**Proof:** Let
|
||||
|
||||
$$
|
||||
F(x)=f(x)-[f(x_{0})+f'(x_{0})(x-x_{0})+\dots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}] \\
|
||||
G(x)=(x-x_{0})^{(n+1)} \\
|
||||
x,x_{0}\in[a,b]
|
||||
$$
|
||||
|
||||
To prove
|
||||
|
||||
$$
|
||||
\frac{F(x)}{G(x)}=\frac{f^{(n+1)}(\xi)}{(n+1)!},\xi\in(a,b)
|
||||
$$
|
||||
|
||||
Clearly, $F(x)$ and $G(x)$ both have continuous derivatives up to $n$th order on $[a, b]$ and have $(n+1)$ st order derivatives on $(a, b)$. Also, $F(x_{0})=F'(x_{0})=\dots=F^{(n)}(x_{0})=0$, $G(x_{0})=G'(x_{0})=\dots=G^{(n)}(x_{0})=0$, and $G^{(n+1)}(x)=(n+1)!$. Hence,
|
||||
|
||||
$$
|
||||
\frac{F(x)}{G(x)}=\frac{F(x)-F(x_{0})}{G(x)-G(x_{0})}=\frac{F'(\xi_{1})}{G'(\xi_{1})}=\frac{F'(\xi_{1})-F'(x_{0})}{G'(\xi_{1})-G'(x_{0})}=\frac{F''(\xi_{2})}{G''(\xi_{2})}=\dots \\=\frac{F^{(n)}(\xi_{n})}{G^{(n)}(\xi_{n})}=\frac{F^{(n)}(\xi_{n})-F^{(n)}(x_{0})}{G^{(n)}(\xi_{n})-G^{(n)}(x_{0})}=\frac{F^{(n+1)}(\xi)}{G^{(n+1)}(\xi)}=\frac{f^{(n+1)}(\xi)}{(n+1)!},\xi\in(a,b)
|
||||
$$
|
||||
|
||||
Proof complete.
|
||||
|
||||
**Note:** Taylor's Theorem can be alternatively stated as follows: if $f(x)$ has \((n+1)\)st order derivatives in a neighborhood $U(x_{0})$ of $x_{0}$, then for any point $x$ in this neighborhood, we have
|
||||
|
||||
$$
|
||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2} \\+ \dots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1},\xi\in(a,b)
|
||||
$$
|
||||
|
||||
This alternative description may be easier to remember.
|
||||
|
||||
The remainder term
|
||||
|
||||
$$
|
||||
R_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}
|
||||
$$
|
||||
|
||||
is called the **Lagrange remainder**, hence Taylor's Theorem can also be called the **Taylor formula with Lagrange remainder**.
|
||||
|
||||
Furthermore, from the conditions of Taylor's Theorem, it can be seen that the conditions for its use are much stricter compared to the Taylor formula (which only requires $n$th order derivatives to exist at a point $x_{0}$), hence the conclusion obtained is stronger. Taylor's Theorem can be utilized to quantitatively approximate the function $f(x)$ using polynomial functions.
|
||||
|
||||
## Taylor Series
|
||||
|
||||
The Taylor series, compared to the two mathematical concepts mentioned earlier, appeared later in mathematical analysis because it requires a foundation in knowledge of series, power series, and function series. Since the knowledge of series and function series is not the focus of this article, interested readers can refer to any textbook on mathematical analysis for further study. Here, we only provide information closely related to the Taylor series, focusing on power series.
|
||||
|
||||
A power series is a type of function series with the simplest form, generated by the sequence of functions $\left\{ a_{n}(x-x_{0})^{n} \right\}$:
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}(x-x_{0})^{n}}=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})^{2}+\dots+a_{n}(x-x_{0})^{n}+\dots
|
||||
$$
|
||||
|
||||
To simplify the form, we only discuss the power series when $x_{0}=0$:
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}=a_{0}+a_{1}x+a_{2}x^{2}+\dots+a_{n}x^{n}+\dots
|
||||
$$
|
||||
|
||||
Correspondingly, by replacing $x$ with $x-x_{0}$, we obtain the general case mentioned above. Hence, the power series mentioned below all refer to the power series:
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
When discussing a function series, the first thing we need to know is its domain of convergence. For a power series, its domain of convergence has a special characteristic, as illustrated in the following theorem:
|
||||
|
||||
**Abel's Theorem:** If the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
converges at $x=\bar{x}\ne0$, then for any $x$ satisfying the inequality $\left| x \right|<\left| \bar{x} \right|$, the power series converges and converges absolutely. If the power series diverges at $x=\bar{x}\ne0$, then for any $x$ satisfying the inequality $\left| x \right|>\left| \bar{x} \right|$, the power series diverges.
|
||||
|
||||
**Proof:** Assume the series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}\bar{x}^{n}}
|
||||
$$
|
||||
|
||||
converges. By the necessary condition for the convergence of series, the sequence $\left\{ a_{n}\bar{x}^{n} \right\}$ converges to zero and is bounded. Hence, there exists a positive number $M$ such that
|
||||
|
||||
$$
|
||||
\left| a_{n}\bar{x}^{n} \right|<M \quad (n=0,1,2,\dots)
|
||||
$$
|
||||
|
||||
Furthermore, for any $x$ satisfying the inequality $\left| x \right|<\left| \bar{x} \right|$, $\left| \frac{x}{\bar{x}} \right|<1$. Thus,
|
||||
|
||||
$$
|
||||
\left| a_{n}x^{n} \right|=\left| a_{n}\bar{x}^{n}\cdot\frac{x^{n}}{\bar{x}^{n}} \right|=\left| a_{n}\bar{x}^{n} \right|\left| \frac{x}{\bar{x}} \right|^{n}<Mr^{n}
|
||||
$$
|
||||
|
||||
where $r=\left| \frac{x}{\bar{x}} \right|<1$. Since the series $\sum_{n=0}^{\infty}{Mr^{n}}$ converges, the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges absolutely when $\left| x \right|<\left| \bar{x} \right|$.
|
||||
|
||||
Conversely, if the power series diverges at $x=\bar{x}\ne0$, and if there exists $x_{0}$ such that $\left| x_{0} \right|>\left| \bar{x} \right|$ and the series $\sum_{n=0}^{\infty}{a_{n}x_{0}^{n}}$ converges, then according to the previous conclusion, the power series should converge absolutely at $x=\bar{x}$, which contradicts the assumption. Thus, for all $x$ satisfying the inequality $\left| x \right|>\left| \bar{x} \right|$, the power series $\sum_{n=0}^{\infty}{a_{n}\bar{x}^{n}}$ diverges.
|
||||
|
||||
In fact, Abel's theorem tells us about the convergence characteristics of power series, that is, the domain of convergence of a power series must be an interval centered at the origin. If we denote the length of this interval as $2R$, then $R$ is called the **radius of convergence** of the power series. We refer to $(-R,R)$ as the **interval of convergence** of the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$.
|
||||
|
||||
**Theorem:** For the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
If $\lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}} = \rho$, then when
|
||||
|
||||
- $(i)$ $0 < \rho < +\infty$, the radius of convergence $R = \frac{1}{\rho}$;
|
||||
- $(ii)$ $\rho = 0$, the radius of convergence $R = +\infty$;
|
||||
- $(iii)$ $p = +\infty$, the radius of convergence $R = 0$.
|
||||
|
||||
**Proof:** For the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{\left| a_{n}x^{n} \right|}
|
||||
$$
|
||||
|
||||
Since
|
||||
|
||||
$$
|
||||
\lim_{n \to \infty}{\sqrt[n]{\left| a_{n}x^{n} \right|}} = \lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}\left| x \right|} = \rho\left| x \right|
|
||||
$$
|
||||
|
||||
According to the root test for positive series, when $\rho\left| x \right| < 1$, $\sum_{n=0}^{\infty}{\left| a_{n}x^{n} \right|}$ converges; when $\rho\left| x \right| > 1$ the power series diverges. Therefore, when $0 < \rho < +\infty$, from $\rho\left| x \right| < 1$, we obtain the radius of convergence $R = \frac{1}{\rho}$. When $\rho = 0$, $\rho\left| x \right| < 1$ holds for any $x$, so $R = +\infty$. When $\rho = +\infty$, $\rho\left| x \right| > 1$ holds for any $x$ except $x = 0$, so $R = 0$.
|
||||
|
||||
**Note:** If
|
||||
|
||||
$$
|
||||
\lim_{n \to \infty}{\frac{\left| a_{n+1} \right|}{\left| a_{n} \right|}} = \rho
|
||||
$$
|
||||
|
||||
then necessarily
|
||||
|
||||
$$
|
||||
\lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}} = \rho
|
||||
$$
|
||||
|
||||
Therefore, in finding the convergence radius, the ratio test can also be utilized. Additionally, in the above proof, we took the absolute value of each term of the original power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ to obtain the power series $\sum_{n=0}^{\infty}{\left| a_{n}x^{n} \right|}$ for demonstration. Since the power series is absolutely convergent within its convergence interval, these two power series have exactly the same convergence radius. Thus, this proof method is effective.
|
||||
|
||||
Certainly, the method mentioned above for finding the convergence radius has limitations. If the limit $\lim_{n \to \infty}{\sqrt[n]{\left| a_{n} \right|}}$ does not exist (and is not positive infinity), then this method will fail. Therefore, in general mathematical analysis textbooks, a more general method for finding the convergence radius of a power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is given using the method of upper limits. Below is the theorem:
|
||||
|
||||
**(Extended) Theorem:** For the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
If
|
||||
|
||||
$$
|
||||
\varlimsup _{n \rightarrow \infty}{\sqrt[n]{\left| a_{n} \right|}}=\rho
|
||||
$$
|
||||
|
||||
then when
|
||||
|
||||
- $(i)$ $0 < \rho < +\infty$, the radius of convergence $R = \frac{1}{\rho}$;
|
||||
- $(ii)$ $\rho = 0$, the radius of convergence $R = +\infty$;
|
||||
- $(iii)$ $p = +\infty$, the radius of convergence $R = 0$.
|
||||
|
||||
Since this upper limit always exists, any power series can be used to find the convergence radius using this theorem.
|
||||
|
||||
In practical problems of finding the convergence radius of power series, we may encounter "missing term" power series, such as the power series
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{\frac{x^{2n}}{n-3^{2n}}}
|
||||
$$
|
||||
|
||||
Such power series can certainly be found using the method of upper limits mentioned above, but a more effective method is to use the root test to deduce the convergence radius of the power series:
|
||||
|
||||
Consider
|
||||
|
||||
$$
|
||||
\lim_{n \rightarrow \infty}{\sqrt[n]{\frac{x^{2n}}{\left| n-3^{2n} \right|}}}=\frac{1}{9}\lim_{n \rightarrow \infty}{\sqrt[n]{\frac{x^{2n}}{1-\frac{n}{3^{2n}}}}}=\frac{x^{2}}{9}
|
||||
$$
|
||||
|
||||
According to the root test for positive series, when $\frac{x^{2}}{9} < 1$, i.e., $\left| x \right| < 3$, the power series converges, and when $\frac{x^{2}}{9} > 1$, i.e., $\left| x \right| > 3$, the power series diverges. When $x = \pm3$, the corresponding series are:
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{\frac{3^{2n}}{n-3^{2n}}}
|
||||
$$
|
||||
|
||||
Since
|
||||
|
||||
$$
|
||||
\lim_{n \rightarrow \infty}{\frac{3^{2n}}{n-3^{2n}}}=-1 \neq 0
|
||||
$$
|
||||
|
||||
the series
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{\frac{3^{2n}}{n-3^{2n}}}
|
||||
$$
|
||||
|
||||
diverges, indicating that the original series has a convergence interval of $(-3,3)$.
|
||||
|
||||
Power series, compared to general series of functions, exhibit two properties regarding uniform convergence:
|
||||
|
||||
**Property 1:** If the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
has a convergence radius $R (> 0)$, then the power series uniformly converges on its convergence interval \((-R,R)\).
|
||||
|
||||
**Proof:** Let $[a,b]$ be any closed interval within $(-R,R)$, and denote
|
||||
|
||||
$$
|
||||
\bar{x} = \max\left\{ \left| a \right|, \left| b \right| \right\} \in (-R,R)
|
||||
$$
|
||||
|
||||
Then for any point $x$ in $[a,b]$, we have
|
||||
|
||||
$$
|
||||
\left| a_{n}x^{n} \right| \leq \left| a_{n}\bar{x}^{n} \right|
|
||||
$$
|
||||
|
||||
Since the power series converges absolutely at the point $\bar{x}$, by the M-test, the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
uniformly converges on $[a,b]$. Since $[a,b]$ was chosen arbitrarily, the power series uniformly converges on the convergence interval $(-R,R)$ .
|
||||
|
||||
**Property 2:** If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ has a convergence radius $R (> 0)$, and converges at $x = R$ (or $x = -R$), then the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ uniformly converges on $[0,R]$ (or $[-R,0]$).
|
||||
|
||||
**Proof:** Suppose the power series converges at $x = R$. For $x \in [0,R]$, we have $\sum_{n=0}^{\infty}{a_{n}x^{n}} = \sum_{n=0}^{\infty}{a_{n}R^{n}(\frac{x}{R})^{n}}$.
|
||||
|
||||
Since the series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}R^{n}}
|
||||
$$
|
||||
|
||||
converges, and the function sequence
|
||||
|
||||
$$
|
||||
\left\{ (\frac{x}{R})^{n} \right\}
|
||||
$$
|
||||
|
||||
is decreasing and uniformly bounded on $[0,R]$, i.e.,
|
||||
|
||||
$$
|
||||
1 \geq \frac{x}{R} \geq (\frac{x}{R})^{n} \geq ... \geq (\frac{x}{R})^{n} \geq ... \geq 0
|
||||
$$
|
||||
|
||||
by Abel's test, the series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
uniformly converges on $[0,R]$.
|
||||
|
||||
**Note:** In fact, since the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is uniformly convergent on $(-R,0]$ , the conclusion can also be drawn: when the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges at $x = R$, the power series uniformly converges on $(-R,R]$.
|
||||
|
||||
From the two properties regarding uniform convergence of power series, we can deduce other properties that power series possess:
|
||||
|
||||
$(i)$ The sum function of the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is continuous on \((-R,R)\).
|
||||
|
||||
$(ii)$ If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges at the left (right) endpoint of its convergence interval, then its sum function is also continuous at this endpoint from the right (left).
|
||||
|
||||
**Note:** Since each term of the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ is continuous on \((-R,R)\), and $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ uniformly converges on \((-R,R)\), we can deduce property $(i)$ from the properties of uniform convergence of series of functions. If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ converges at $x = R$ (or $x = -R$), then the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ uniformly converges on $[0,R]$ (or $[-R,0]$) by the same reasoning, thus property $(ii)$ holds.
|
||||
|
||||
In the study of series of functions, there are theorems concerning term-by-term integration and differentiation:
|
||||
|
||||
**(Term-by-term Integration Theorem):** If the series of functions
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
||||
$$
|
||||
|
||||
uniformly converges on $[a,b]$, and each term $u_{n}(x)$ is continuous, then
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{\int_{a}^{b}u_{n}(x)dx}=\int_{a}^{b}\sum_{n=0}^{\infty}{u_{n}(x)dx}
|
||||
$$
|
||||
|
||||
**(Term-by-term Differentiation Theorem):** If the series of functions
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
||||
$$
|
||||
|
||||
has continuous derivative for each term on $[a,b]$, $x_{0}\in[a,b]$ is a point of convergence for
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
||||
$$
|
||||
|
||||
, and
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{u'_{n}(x)}
|
||||
$$
|
||||
|
||||
uniformly converges on $[a,b]$, then
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}({\frac{d}{dx}u_{n}(x)})=\frac{d}{dx}(\sum_{n=0}^{\infty}{u_{n}(x)})
|
||||
$$
|
||||
|
||||
**Note:** The requirement that $x_{0}\in[a,b]$ is a point of convergence for
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
||||
$$
|
||||
|
||||
in the term-by-term differentiation theorem is for the convenience of application. Its equivalent condition is that
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{u_{n}(x)}
|
||||
$$
|
||||
|
||||
converges on $[a,b]$. Furthermore, the interval $[a,b]$ in the conditions can be replaced with a general open interval, and the conclusion still holds.
|
||||
|
||||
For the power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
its power series obtained by differentiating each term is
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{na_{n}x^{n-1}}
|
||||
$$
|
||||
|
||||
and the power series obtained by integrating each term is
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{\frac{a_{n}x^{n+1}}{n+1}}
|
||||
$$
|
||||
|
||||
For convenience, let's denote the three power series as $(1)$, $(2)$, and $(3)$, respectively.
|
||||
|
||||
To discuss term-by-term differentiation and integration of power series, we first introduce the following lemma:
|
||||
|
||||
**Lemma:** Power series $(1)$ and $(2)$, $(3)$ have the same interval of convergence.
|
||||
|
||||
**Proof:** We only need to prove that $(1)$ and $(2)$ have the same interval of convergence because differentiating each term of $(3)$ results in $(2)$.
|
||||
|
||||
Suppose $(1)$ converges only at $x=0$. Assuming $(2)$ converges at $x'>0$, then for $\bar{x}\in(0,x')$, by the Abel's theorem,
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{\left| na_{n}\bar{x}^{n-1} \right|}
|
||||
$$
|
||||
|
||||
converges. Thus,
|
||||
|
||||
$$
|
||||
\left| a_{n}\bar{x}^{n}\right|=\left| na_{n}\bar{x}^{n-1} \right|\left| \frac{\bar{x}}{n} \right|=\left| na_{n}\bar{x}^{n-1} \right|\frac{\bar{x}}{n}
|
||||
$$
|
||||
|
||||
Since it is given that
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{\left| na_{n}\bar{x}^{n-1} \right|}
|
||||
$$
|
||||
|
||||
converges,
|
||||
|
||||
$$
|
||||
\left\{ \frac{\bar{x}}{n} \right\}
|
||||
$$
|
||||
|
||||
is monotonically bounded. Thus, by the Abel's test, we know that
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty}{\left| a_{n}\bar{x}^{n} \right|}
|
||||
$$
|
||||
|
||||
converges. This contradicts the assumption. Therefore, $(2)$ also converges only at $x=0$, and the proposition holds.
|
||||
|
||||
Now let the convergence interval of power series $(1)$ be $(-R,R)$, where $R\neq 0$. Let $x_{0}$ be any nonzero point in $(-R,R)$. As shown in the proof of the Abel's theorem, there exist positive numbers $M$ and $r(0<r<1)$ such that for all positive integers $n$,
|
||||
|
||||
$$
|
||||
\left| a_{n}x_{0}^{n} \right|<Mr^{n}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\left| na_{n}x_{0}^{n-1} \right|=\left| \frac{n}{x_{0}} \right|\left| a_{n}x_{0}^{n} \right|<\frac{M}{\left| x_{0} \right|}nr^{n}
|
||||
$$
|
||||
|
||||
By the ratio test, the series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{nr^{n}}
|
||||
$$
|
||||
|
||||
converges. Therefore, by the comparison test, the series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{\left| na_{n}x_{0}^{n-1} \right|}
|
||||
$$
|
||||
|
||||
converges. This implies that power series $(2)$ is absolutely convergent (and hence convergent) at point $x_{0}$, as it converges absolutely. Since $x_{0}$ is an arbitrary point in $(-R,R)$, power series $(2)$ converges on the interval $(-R,R)$.
|
||||
|
||||
Next, we need to prove that power series $(2)$ does not converge for all $x$ satisfying $\left| x \right|>R$. Suppose $(2)$ converges at a point $x_{0} (\left| x_{0} \right|>R)$, then there exists a number $\bar{x}$ such that $\left| x_{0} \right|>\left| \bar{x} \right|>R$. By the Abel's theorem, power series $(2)$ converges absolutely at $x=\bar{x}$. However, when $n\geq\left| \bar{x} \right|$, we have
|
||||
|
||||
$$
|
||||
\left| na_{n}\bar{x}^{n-1} \right|=\frac{n}{\left| \bar{x} \right|}\left| a_{n}\bar{x}^{n} \right|\geq \left| a_{n}\bar{x}^{n} \right|
|
||||
$$
|
||||
|
||||
By the comparison test, power series $(1)$ converges absolutely at $x=\bar{x}$. This contradicts the fact that the convergence interval of power series $(1)$ is $(-R,R)$. Thus, power series $(2)$ does not converge for all $x$ satisfying $\left| x \right|>R$. In summary, power series $(1)$ and $(2)$ have the same interval of convergence.
|
||||
|
||||
Regarding term-by-term differentiation and integration of power series, we have the following theorem:
|
||||
|
||||
**Theorem:** Suppose the convergence interval of series $(1)$ is $(-R, R)$, and its sum function on this interval is denoted by $f(x)$. If $x$ is any point in $(-R, R)$, then:
|
||||
|
||||
- $(i)$ $f(x)$ is differentiable at point $x$, and
|
||||
$$
|
||||
f'(x)=\sum_{n=1}^{\infty}{na_{n}x^{n-1}}
|
||||
$$
|
||||
- $(ii)$ $f(x)$ is integrable over the interval between $0$ and $x$ on $(-R, R)$, and
|
||||
$$
|
||||
\int_{0}^{x}f(t)dt=\sum_{n=0}^{\infty}{\frac{a_{n}}{n+1}x^{n+1}}
|
||||
$$
|
||||
|
||||
**Proof:** Since series $(1)$, $(2)$, and $(3)$ have the same convergence radius $R$, and each term of series $(1)$ has a continuous derivative, and all three power series converge uniformly on the closed interval $(-R, R)$, they satisfy the theorem of term-by-term differentiation and integration of function series. Therefore, the above theorem holds.
|
||||
|
||||
From the above theorem, we can derive the following corollaries:
|
||||
|
||||
**Corollary 1:** Let $f(x)$ be the sum function of series $(1)$ on the convergence interval $(-R, R)$. Then, $f(x)$ has derivatives of any order on $(-R, R)$, and can be differentiated term by term any number of times, i.e.,
|
||||
|
||||
$$
|
||||
f'(x)=a_{1}+2a_{2}x+3a_{3}x^{2}+...+na_{n}x^{n-1}+...
|
||||
$$
|
||||
|
||||
$$
|
||||
f''(x)=2a_{2}+3\cdot2a_{3}x+...+n(n-1)a_{n}x^{n-2}+...
|
||||
$$
|
||||
|
||||
$$
|
||||
f^{(n)}(x)=n!a_{n}+(n+1)n(n-1)...2a_{n+1}x+...
|
||||
$$
|
||||
|
||||
**Corollary 2:** Let $f(x)$ be the sum function of series $(1)$ on the convergence interval $(-R, R)$. Then the coefficients of series $(1)$ are determined by the various derivatives of $f(x)$ at $x=0$:
|
||||
|
||||
$$
|
||||
a_{0}=f(0) \\ a_{n}=\frac{f^{(n)}(0)}{n!} \quad (n=1,2,...)
|
||||
$$
|
||||
|
||||
**Equality of Power Series:** If the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ and $\sum_{n=0}^{\infty}{b_{n}x^{n}}$ have the same sum function in a neighborhood of $x=0$, then these two power series are considered equal in that neighborhood.
|
||||
|
||||
Since the coefficients of power series are determined by the sum function and its derivatives at $x=0$, it follows from the definition of equality of power series that two power series are equal in a neighborhood if and only if their coefficients are equal.
|
||||
|
||||
**Arithmetic Operations on Power Series:** Suppose the power series $\sum_{n=0}^{\infty}{a_{n}x^{n}}$ and $\sum_{n=0}^{\infty}{b_{n}x^{n}}$ have convergence radii $R_{a}$ and $R_{b}$, respectively. Then:
|
||||
|
||||
- $(i)$ $\lambda\sum_{n=0}^{\infty}{a_{n}x^{n}}=\sum_{n=0}^{\infty}{\lambda a_{n}x^{n}},\left| x \right|<R$ ;
|
||||
- $(ii)$ $\sum_{n=0}^{\infty}{a_{n}x^{n}}\pm\sum_{n=0}^{\infty}{b_{n}x^{n}}=\sum_{n=0}^{\infty}{(a_{n}\pm b_{n})x^{n}},\left| x \right|<R$ ;
|
||||
- $(iii)$ $(\sum_{n=0}^{\infty}{a_{n}x^{n}})(\sum_{n=0}^{\infty}{b_{n}x^{n}})=\sum_{n=0}^{\infty}{c_{n}x^{n}},\left| x \right|<R$ .
|
||||
|
||||
where $\lambda$ is a constant, and $R=\min\{ R_{a}, R_{b} \}$, $c_{n}=\sum_{k=0}^{n}{a_{k}b_{n-k}}$.
|
||||
|
||||
These properties can be derived from the corresponding properties of numerical series.
|
||||
|
||||
The above discussion regarding power series actually serves as a preliminary study for Taylor series. Although it might seem extensive, it's essential for understanding Taylor series thoroughly.
|
||||
|
||||
In the section on Taylor's theorem, we previously mentioned that if a function $f(x)$ has derivatives up to order $n + 1$ in a neighborhood of $x_{0}$, then the Taylor series expansion is given by:
|
||||
|
||||
$$
|
||||
f(x) = f(x_{0}) + f'(x_{0})(x-x_{0}) + \frac{f''(x_{0})}{2!}(x-x_{0})^{2} + \ldots + \frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n} + R_{n}(x)
|
||||
$$
|
||||
|
||||
Here, $R_{n}(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}$, where $\xi$ lies between $x$ and $x_{0}$.
|
||||
|
||||
Inspired by the form of Taylor's theorem, if a function $f(x)$ has derivatives of all orders at $x = x_{0}$, then we can construct a power series:
|
||||
|
||||
$$
|
||||
f(x_{0}) + f'(x_{0})(x-x_{0}) + \frac{f''(x_{0})}{2!}(x-x_{0})^{2} + \ldots + \frac{f^{(n)}(x-x_{0})^{n}}{n!} + \ldots
|
||||
$$
|
||||
|
||||
This series is called the **Taylor series** of the function $f(x)$ at the point $x_{0}$. Now, we face the question: What is the relationship between the function $f(x)$ and its Taylor series expansion at $x_{0}$? If the function $f(x)$ is defined in a neighborhood $U(x_{0},\delta)$ and its Taylor series converges in the interval $U(x_{0},R)$, does the function $f(x)$ equal the sum function of its Taylor series in $U(x_{0},\delta)\cap U(x_{0},R)$?
|
||||
|
||||
**Theorem:** Suppose $f(x)$ has derivatives of all orders at the point $x_{0}$. Then, $f(x)$ equals the sum function of its Taylor series on the interval $(x_{0}-r,x_{0}+r)$ if and only if, for all $x$ satisfying $|x-x_{0}|<r$, we have
|
||||
|
||||
$$
|
||||
\lim_{n \rightarrow \infty}{R_{n}(x)} = 0
|
||||
$$
|
||||
|
||||
Here, $R_{n}(x)$ represents the Lagrange remainder term of $f(x)$ at $x_{0}$.
|
||||
|
||||
**Proof:** Given that $f(x)$ has derivatives of all orders at $x_{0}$, by Taylor's theorem, for any $x \in U(x_{0},r)$, where $r \leq R$, we have $f(x) = T_{n}(x) + R_{n}(x)$.
|
||||
|
||||
**[Necessity]:** If $f(x) = \lim_{n \rightarrow \infty}{T_{n}(x)}$, then as $n \rightarrow \infty$, we have $\lim_{n \rightarrow \infty}{R_{n}(x)} = 0$.
|
||||
|
||||
**[Sufficiency]:** If $\lim_{n \rightarrow \infty}{R_{n}(x)} = 0$, then $f(x) = \lim_{n \rightarrow \infty}{T_{n}(x)}$.
|
||||
|
||||
## Taylor Expansion
|
||||
|
||||
If function $f(x)$ can be expressed as the sum function of its Taylor series in a neighborhood of point $x*{0}$, then function $f(x)$ can be expanded into a Taylor series in the neighborhood of point $x*{0}$. The right side of the equation
|
||||
|
||||
$$
|
||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+...+\frac{f^{(n)}(x_{0})^{n}}{n!}+...
|
||||
$$
|
||||
|
||||
is called the **Taylor expansion** of $f(x)$ at point $x_{0}$.
|
||||
|
||||
According to the previous theorem, if function $f(x)$ is the sum function of a power series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}{a_{n}x^{n}}
|
||||
$$
|
||||
|
||||
in the convergence interval $(-R, R)$, then the coefficients of $\sum*{n=0}^{\infty}{a*{n}x^{n}}$ are determined by the sum function $f(x)$ and the values of its various order derivatives at $x=0$, that is,
|
||||
|
||||
$$
|
||||
a_{0}=f(0) \\ a_{n}=\frac{f^{(n)}(0)}{n!} \\ n=1,2,...
|
||||
$$
|
||||
|
||||
That is, $\sum*{n=0}^{\infty}{a*{n}x^{n}}$ is the Taylor expansion of function $f(x)$ on $(-R, R)$.
|
||||
|
||||
The above is the process of analyzing these four mathematical concepts. In the part of Taylor series, the relevant concepts of power series are elaborated in detail. Here we summarize these four concepts:
|
||||
|
||||
**Summary:** From the chronological point of view, we usually encounter the Taylor formula for the first time in the part of the mean value theorem of differentiation in the first volume of mathematical analysis, that is, the Taylor formula with the Peano remainder term, which is introduced by the finite increment formula in the derivative:
|
||||
|
||||
$$
|
||||
f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})
|
||||
$$
|
||||
|
||||
When using the finite increment formula for estimation, the error is $o(x-x*{0})$, and its estimation effect is quite rough. If the function is known to have an $n$-th order derivative at the point $x*{0}$, we can generalize the finite increment formula, that is, to obtain the Taylor formula with the Peano remainder term. Its estimation error is $o((x-x*{0})^{n})$. In order to further improve the estimation effect and quantitatively analyze the range of errors, the Taylor formula with the Lagrange remainder term is introduced. The use condition of Taylor formula with the Lagrange remainder term is further strict, which requires that the function $f(x)$ has derivatives up to $(n+1)$-th order at the point $x*{0}$. Its corresponding error is
|
||||
|
||||
$$
|
||||
\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}
|
||||
$$
|
||||
|
||||
The Lagrange remainder term can quantitatively analyze the error, and its estimation effect is much better than that of the Peano remainder term.
|
||||
|
||||
Following the learning order of the textbook, after learning related knowledge such as series, functional series, and power series in the second volume of mathematical analysis, we can introduce the concept of Taylor series. If the function $f(x)$ has derivatives of any order at some point $x_{0}$, then we can write
|
||||
|
||||
$$
|
||||
f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+...+\frac{f^{(n)}(x_{0})^{n}}{n!}+...
|
||||
$$
|
||||
|
||||
This expression is called the Taylor series of function $f(x)$ at point $x*{0}$. As a special power series, the Taylor series has a convergence range, namely the convergence domain of the Taylor series, and we give the necessary and sufficient conditions for the Taylor series of function $f(x)$ at point $x*{0}$ in a certain neighborhood $U(x*{0},r)$ to be equal to its sum function: $\lim*{n \rightarrow \infty}{R_{n}(x)}=0$.
|
||||
|
||||
This leads to the concept of Taylor expansion. The so-called Taylor expansion refers to the power series expression that function $f(x)$ can be expanded into in a certain neighborhood. In this neighborhood, function $f(x)$ is completely characterized by the power series. This is different from the approximation by polynomial functions above, but is equal in a real sense. However, the application of power series has certain limitations, namely, because the convergence domain of power series is often a finite interval, it can only characterize function $f(x)$ in a small segment interval. In order to solve this drawback of power series, research on Fourier series has emerged.
|
||||
195
data/posts/2024-03-12-data-table-relations-normalization.md
Normal file
195
data/posts/2024-03-12-data-table-relations-normalization.md
Normal file
@@ -0,0 +1,195 @@
|
||||
---
|
||||
title: "Data Table Relation's Normalization"
|
||||
subtitle: ""
|
||||
summary: "Introduces functional dependencies, and the database paradigms 1NF, 2NF, 3NF, BCNF, and 4NF. and use examples to explain their concepts and connections."
|
||||
coverURL: ""
|
||||
time: "2024-03-12"
|
||||
tags: ["database"]
|
||||
noPrompt: false
|
||||
pin: false
|
||||
allowShare: true
|
||||
---
|
||||
|
||||
## Functional Dependencies
|
||||
|
||||
In relational databases, functional dependencies describe the dependency relationships between attributes in a relational schema. If, given a relation $R$, the values of attribute set $X$ uniquely determine (through conditions or function arguments, for example) a value in attribute set $Y$, then we say that $Y$ is functionally dependent on $X$, typically denoted by the symbol $X \rightarrow Y$.
|
||||
|
||||
Specifically, if for every record in relation $R$, whenever two records have the same values for attribute set $X$, they must also have the same values for attribute set $Y$, then we say that $Y$ is functionally dependent on $X$.
|
||||
|
||||
For example, suppose we have a relation $R$ containing attribute set $\{ A,B,C \}$, where the values of attribute $A$ uniquely determine the values of attribute $B$, i.e., $A \rightarrow B$. Then, we say that attribute $B$ is functionally dependent on attribute $A$.
|
||||
|
||||
Functional dependency is an important concept in relational database design. It helps in understanding the relationships between data, normalizing database designs to reduce redundant data, while ensuring the consistency and integrity of data.
|
||||
|
||||
Functional dependencies can be classified into trivial functional dependencies and non-trivial functional dependencies.
|
||||
|
||||
If $X \rightarrow Y$ and $Y \subseteq X$, then $X \rightarrow Y$ is called a trivial functional dependency. Otherwise, it is a non-trivial functional dependency.
|
||||
|
||||
For functional dependencies, the dependency relationship between $X$ and $Y$ can also be further classified into partial functional dependency, full functional dependency, and transitive functional dependency.
|
||||
|
||||
- Partial Functional Dependency: Let $X,Y$ be two attribute sets of relation $R$. If $X→Y$ and $X' \subsetneq X$, where there exists $X'$ such that $X'→Y$, then $Y$ is said to be partially functionally dependent on $X$, denoted as $X \overset{P}{\rightarrow} Y$. In other words, partial functional dependency means that some attributes can be removed without affecting the dependency.
|
||||
|
||||
> For example: In a student basic information table $R$ (student ID, passport number, name), of course, the student ID attribute values are unique. In relation $R$, (student ID, passport number) → (name), (student ID) → (name), (passport number) → (name); therefore, the name is partially functionally dependent on (student ID, passport number).
|
||||
|
||||
- Full Functional Dependency: Let $X,Y$ be two attribute sets of relation $R$. If $X→Y$, $X' \subsetneq X$, and for all $X'$, $X'→Y$, then $Y$ is said to be fully functionally dependent on $X$, denoted as $X \overset{F}{\rightarrow} Y$. In other words, for full functional dependency, no extra attributes can be deleted, otherwise, the property of dependency will not be maintained.
|
||||
|
||||
> Example: In a student basic information table $R$ (student ID, class, name), assuming different classes can have the same student ID, and student IDs within a class cannot be the same. In relation $R$, (student ID, class) → (name), but (student ID) → (name) does not hold, and (class) → (name) does not hold either. Therefore, the name is fully functionally dependent on (student ID, class).
|
||||
|
||||
- Transitive Functional Dependency: Let $X,Y,Z$ be three attribute sets of relation $R$, where $X→Y (Y \cancel{\rightarrow} X)$, and for all $Y$, $Y→Z$. Then $Z$ is said to be transitively functionally dependent on $X$. This means that $Z$ indirectly depends on $X$.
|
||||
|
||||
> Example: In relation $R$ (student ID, dormitory, fee), (student ID) → (dormitory), dormitory ≠ student ID, (dormitory) → (fee), fee ≠ dormitory. Thus, it meets the requirements of transitive functional dependency.
|
||||
|
||||
## Multi-Valued Dependencies
|
||||
|
||||
The previous section introduced functional dependencies, which are actually a special case of multi-valued dependencies. Multi-valued dependencies extend the concept of functional dependencies.
|
||||
|
||||
Let $R(U)$ be a relational schema over the attribute set $U$, and let $X$, $Y$, and $Z$ be subsets of $U$ such that $Z = U - X - Y$. A multi-valued dependency $X \twoheadrightarrow Y$ holds if and only if for any relation $r$ in $R$, each value on $(X, Z)$ corresponds to a set of values on $Y$, and this set of values depends only on the values of $X$ and is independent of the values of $Z$.
|
||||
|
||||
Consider a relational schema $R$ with the attribute set $\{Student, Course, Textbook\}$, representing students' course enrollments and the textbooks they use. If a student uses multiple textbooks for a single course, and the combination of student and course uniquely determines the textbooks used, while the combination of student and course is independent, then we have a multi-valued dependency.
|
||||
|
||||
Suppose we have the following relation instance:
|
||||
|
||||
| Student | Course | Textbook |
|
||||
| ------- | ------- | -------------- |
|
||||
| Alice | Math | Calculus |
|
||||
| Alice | Math | Linear Algebra |
|
||||
| Alice | Physics | Mechanics |
|
||||
| Bob | Math | Calculus |
|
||||
|
||||
In this example, the choice of textbook depends on the combination of student and course. For instance, Alice uses both Calculus and Linear Algebra textbooks for her Math course, while she uses Mechanics for her Physics course. However, whether Linear Algebra and Calculus are chosen depends solely on whether the course is Math.
|
||||
This scenario demonstrates a multi-valued dependency, where the combination of student and course uniquely determines the set of textbooks used, while the relationship between student and course is independent, yet textbooks are not independent of courses as one course can have multiple textbooks.
|
||||
|
||||
Therefore, in this scenario, there exists a multi-valued dependency relationship $Course \twoheadrightarrow Textbook$.
|
||||
|
||||
## Keys
|
||||
|
||||
- Let $K$ be an attribute or a combination of attributes in $R<U, F>$, and $K \overset{F}{\rightarrow} U$, then $K$ is a candidate key for $R$.
|
||||
- If there are multiple candidate keys, one of them can be designated as the primary key.
|
||||
- Any attribute set that contains a candidate key is called a prime attribute. Otherwise, it is a non-prime attribute.
|
||||
- If the entire attribute set constitutes the candidate key, then this attribute set is called a superkey.
|
||||
- Both primary keys and candidate keys are commonly referred to as keys.
|
||||
|
||||
## Database Normalization
|
||||
|
||||
### 1NF
|
||||
|
||||
$1NF$ (First Normal Form) is one of the fundamental normal forms in relational databases. It requires that each attribute in a relation schema is atomic, meaning it cannot be further divided. In other words, each attribute in the relation schema should be single-valued, rather than containing multiple values or complex data types.
|
||||
|
||||
Specifically, $1NF$ requires that each cell in the relation contains only one value, rather than multiple values or complex data types. This helps ensure the atomicity of data, simplifying data processing and querying.
|
||||
|
||||
For example, consider a student table containing names and phone numbers. If phone numbers are stored as a comma-separated list of multiple numbers, then this table does not conform to $1NF$. To adhere to $1NF$, phone numbers should be split into separate attributes, with each attribute containing only one phone number.
|
||||
|
||||
### 2NF
|
||||
|
||||
$2NF$ (Second Normal Form) is another normal form in relational databases, built upon the foundation of the first normal form ($1NF$). $2NF$ requires that each non-prime attribute in a relation schema is fully functionally dependent on the candidate key, rather than partially dependent on the candidate key.
|
||||
|
||||
Specifically, if a relation schema has multiple attributes forming the candidate key, then each non-prime attribute should depend on all combinations of these attributes, rather than just depending on some of them.
|
||||
|
||||
For example, consider a relation schema containing the following attributes: StudentID, CourseID, CourseName, StudentName, and Grade. In this schema, (StudentID, CourseID) forms the candidate key, representing the enrollment of students in courses.
|
||||
|
||||
| StudentID | CourseID | CourseName | StudentName | Grade |
|
||||
| --------- | -------- | ---------- | ----------- | ----- |
|
||||
| 101 | 001 | Math | Alice | A |
|
||||
| 101 | 002 | Physics | Alice | B |
|
||||
| 102 | 001 | Math | Bob | A |
|
||||
| 102 | 003 | Chemistry | Bob | C |
|
||||
|
||||
In this example, the StudentName attribute is a non-prime attribute and is partially dependent on the candidate key (StudentID), rather than fully dependent on all attributes of the candidate key (StudentID, CourseID). For instance, the name of student Alice is only associated with Student ID 101, irrespective of the course enrollment.
|
||||
|
||||
Therefore, this relation schema does not satisfy the second normal form ($2NF$). To adhere to $2NF$, we should remove the StudentName attribute from this relation schema and place it in a separate table, where the candidate key is $StudentID$. This way, the student name becomes fully dependent on the candidate key, rather than partially dependent on it.
|
||||
|
||||
### 3NF
|
||||
|
||||
Given a relation schema $R<U,F> \in 1NF$ and no set of attributes $X$, attribute group $Y$, and non-candidate attribute $Z$ such that $X \rightarrow Y, Y \rightarrow Z, Y \cancel{\rightarrow} X$, it belongs to $3NF$. In other words, if a relation is in $2NF$ and each non-candidate attribute does not transitively depend on the candidate key, then it is in $3NF$.
|
||||
|
||||
Let's continue with the example of student course enrollment mentioned earlier and attempt to conform to the third normal form ($3NF$).
|
||||
|
||||
In this example, we have already removed the student name from the main table and placed it in a separate table as follows:
|
||||
|
||||
**Student Table**:
|
||||
|
||||
| StudentID | StudentName |
|
||||
| --------- | ----------- |
|
||||
| 101 | Alice |
|
||||
| 102 | Bob |
|
||||
|
||||
**Enrollment Table**:
|
||||
|
||||
| StudentID | CourseID | Grade |
|
||||
| --------- | -------- | ----- |
|
||||
| 101 | 001 | A |
|
||||
| 101 | 002 | B |
|
||||
| 102 | 001 | A |
|
||||
| 102 | 003 | C |
|
||||
|
||||
Now, let's see if it conforms to $3NF$. In this relation schema, we have a transitive dependency: Student ID (StudentID) determines Student Name (StudentName), while Course ID (CourseID) determines Student ID (StudentID). Hence, there exists a transitive functional dependency: $CourseID \rightarrow StudentName$.
|
||||
|
||||
To conform to $3NF$, we need to eliminate this transitive dependency. One way to do this is by creating a new table that maps $CourseID$ and $StudentID$ to $StudentName$ to eliminate this transitive dependency. This way, we can ensure that each non-prime attribute is fully dependent on the primary key.
|
||||
|
||||
**Student Enrollment Relation Table**:
|
||||
|
||||
| StudentID | CourseID | Grade |
|
||||
| --------- | -------- | ----- |
|
||||
| 101 | 001 | A |
|
||||
| 101 | 002 | B |
|
||||
| 102 | 001 | A |
|
||||
| 102 | 003 | C |
|
||||
|
||||
**Student Table**:
|
||||
|
||||
| StudentID | StudentName |
|
||||
| --------- | ----------- |
|
||||
| 101 | Alice |
|
||||
| 102 | Bob |
|
||||
|
||||
**Course Table**:
|
||||
|
||||
| CourseID | CourseName |
|
||||
| -------- | ----------- |
|
||||
| 001 | Mathematics |
|
||||
| 002 | Physics |
|
||||
| 003 | Chemistry |
|
||||
|
||||
Now, each table conforms to the third normal form ($3NF$). The student table and the course table are associated with the student enrollment relation table without any transitive dependency.
|
||||
|
||||
### BCNF
|
||||
|
||||
$BCNF$ (Boyce-Codd Normal Form) is a more stringent form of normalization in relational databases, resulting from normalizing relation schemas further from the third normal form ($3NF$). $BCNF$ requires that every non-trivial functional dependency (non-trivial $X \rightarrow Y$, where $Y$ is not a superset of $X$) is determined by the keys of the relation.
|
||||
|
||||
In other words, if $R$ is a relation schema and $X \rightarrow Y$ is a non-trivial functional dependency of $R$, and $X$ does not contain any candidate keys, then $R$ does not conform to $BCNF$, meaning every determinant must include a key.
|
||||
|
||||
For example, consider a scheduling table now, recording student ID, course ID, and teacher ID. A teacher teaches only one course, and a course can be taught by multiple teachers, and each student selects a specific course, which corresponds to a fixed teacher. Assuming the candidate key is student ID, course ID. We can list the following functional relationships:
|
||||
|
||||
- $(StudentID,CourseID) \rightarrow TeacherID$
|
||||
- $(StudentID,TeacherID) \rightarrow CourseID$
|
||||
- $TeacherID \rightarrow CourseID$
|
||||
|
||||
This relation does not conform to $BCNF$ because we find that in the third functional dependency, $TeacherID$ does not contain any keys. While the first and second have keys.
|
||||
|
||||
### 4NF
|
||||
|
||||
$4NF$ is a form of database normalization that further emphasizes the elimination of multi-valued dependencies on top of $BCNF$. A relation schema satisfies $4NF$ if, in addition to satisfying the requirements of $BCNF$, it also has no non-trivial multi-valued dependencies. Non-trivial multi-valued dependencies refer to those where neither the left side nor the right side is a superkey of the relation.
|
||||
|
||||
Let's consider an example that complies with $BCNF$ but not with $4NF$.
|
||||
|
||||
Suppose we have a relation schema $R$ containing attributes: Student, Course, Grade, and Teacher. And there exist the following functional dependencies:
|
||||
|
||||
1. $(Student, Course) \rightarrow Grade$
|
||||
2. $Course \rightarrow Teacher$
|
||||
3. $Student \twoheadrightarrow Teacher$
|
||||
|
||||
Assume that the candidate key for the relation schema is $Student, Course$.
|
||||
|
||||
This schema conforms to $BCNF$ because every functional dependency is determined by the candidate key.
|
||||
|
||||
However, it does not conform to $4NF$ due to the presence of the third multi-valued dependency. This is because each student may attend multiple courses, and each course may have different teachers.
|
||||
|
||||
Therefore, although this relation schema satisfies $BCNF$, it does not satisfy $4NF$.
|
||||
|
||||
### Relationship
|
||||
|
||||
Understanding from $1NF$ to $4NF$ is progressive. The relationship between them is as follows:
|
||||
|
||||
- $1NF$ eliminates partial functional dependencies of non-prime attributes on the candidate key to achieve $2NF$.
|
||||
- $2NF$ eliminates transitive functional dependencies of non-prime attributes on the candidate key to achieve $3NF$.
|
||||
- $3NF$ eliminates partial and transitive functional dependencies of prime attributes on the candidate key to achieve $BCNF$.
|
||||
- $BCNF$ eliminates non-trivial and functional dependencies of multi-valued dependencies to achieve $4NF$.
|
||||
Reference in New Issue
Block a user